HYPEROCTAÈDRE DE DIMENSION 4
16-cell, 16-Zeller
| polyèdre suivant | polyèdre précédent | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
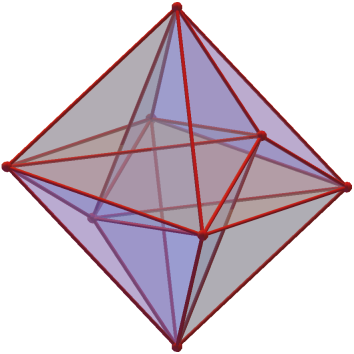
HYPEROCTAÈDRE DE DIMENSION 4
16-cell, 16-Zeller

L'hyperoctaèdre de dimension 4 est l'analogue en
dimension 4 de l'octaèdre
en dimension 3.
| Autres noms | 4-cocube, "16 cellules", C16, hexadécachore, hexadécatope, 4-orthoplexe |
| Famille | polychore régulier et cocube |
| Dual | hypercube de dimension 4 |
| Symbole de Schläfli | {3, 3, 4} (4 tétraèdres autour de chaque arête) |
| Cellules | 16 tétraèdres |
| Faces | 32 triangles |
| Arêtes | 24 arêtes de longueur a appartenant chacune à 4 faces et à 3 cellules. |
| Sommets | 8 sommets appartenant chacun à 6 arêtes, 12 faces, et 8 cellules. |
| Base de calotte | octaèdre |
| Patron |
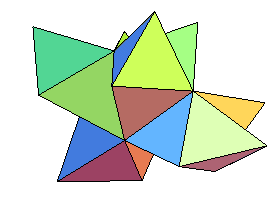 |
| Graphe des arêtes |
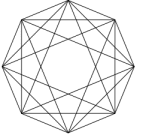 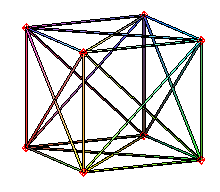
graphe complet |
| Diamètres | hypersphère inscrite : a / |
| Mensurations | hypervolume de l'hyperoctaèdre plein : volume de sa frontière : |
| Coordonnées
des sommets |
( Les 4 sommets d'une cellule sont formés de 4 points où la coordonnée non nulle n'est pas à la même place. Équation cartésienne de l'hyperoctaèdre plein : |
|
Groupe des isométries |
ordre 384 = 27.3 = 24.4! |
| Pavage | L'hyperoctaèdre pave l'espace de dimension 4. |
| Sites | fr.wikipedia.org/wiki/Hexadécachore
www.polytope.de/c16.html |
| De la dimension 1 à la dimension 2, un segment (1-cocube) devient un carré (2-cocube) | De la dimension 2 à la dimension 3, un carré (2-cocube) devient un octaèdre (3-cocube) | De la dimension 3 à la dimension 4, un octaèdre (3-cocube) devient un hyperoctaèdre (4-cocube) |
 |
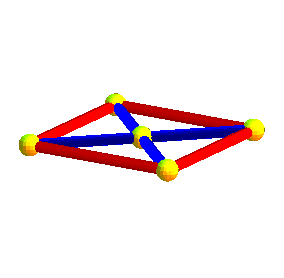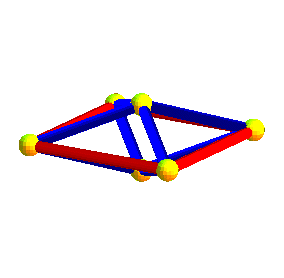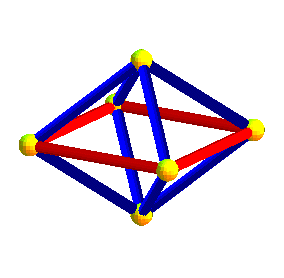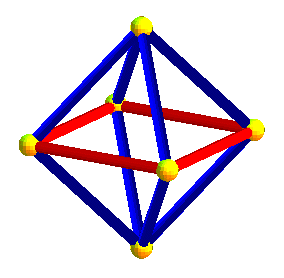 |

de même que l'octaèdre est formé de deux pyramides à bases carrées, l'hyperoctaèdre est formé de deux hyperpyramides à bases octaédrales |
Dans les animations ci-dessus, trois des projetés des axes de symétrie de l'hyperoctaèdre sont deux à deux orthogonaux, mais le projeté du 4ème n'est pas orthogonal aux autres ; dans les animations ci-dessous, les projetés des 4 axes sont équirépartis suivant les diagonales d'un cube ; défaut : les carrés et octaèdres nne sont plus réguliers...
 |
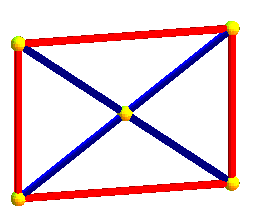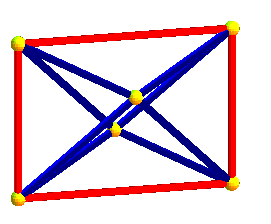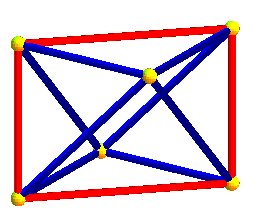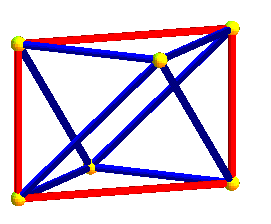 |
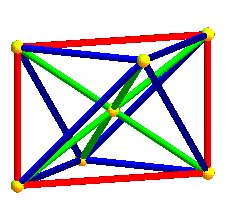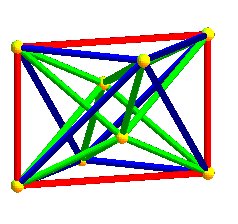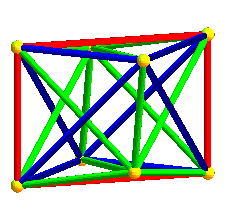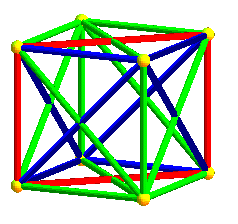 |
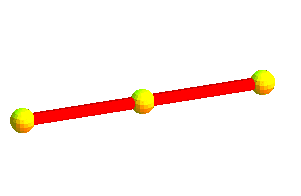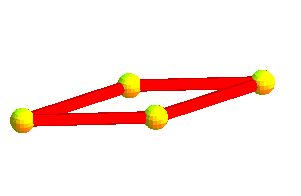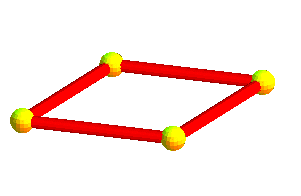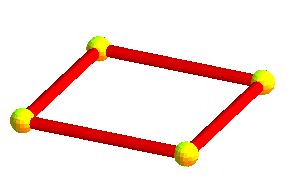
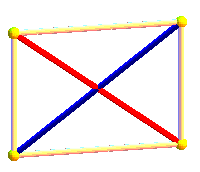
| De même que le carré (2-cocube) est formé d'une armature... | et que l'octaèdre (3-cocube) est formé d'une armature ... | |||
...de deux segments orthogonaux
 |
|
|
|
|||
|
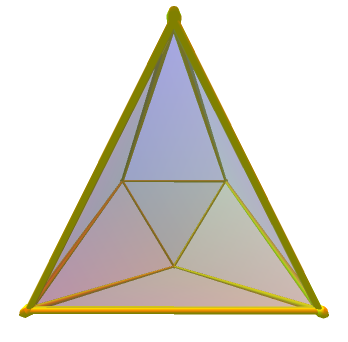
| De même que la perspective (c'est-à-dire la perspective conique plane) d'un octaèdre sur un plan parallèle à une face donne la figure ci-dessous (un triangle inséré dans un triangle), | la perspective conique d'un hyperoctaèdre 4D sur un hyperplan parallèle à une cellule, elle même projetée (affinement cette fois) sur un plan, donne la figure ci-dessous (un tétraèdre inséré dans un tétraèdre). |
 |
 |
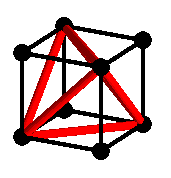
| De même que le tétraèdre est un demi-cube, | l'hyperoctaèdre est un demi-hypercube, en ce sens qu'on peut le construire en ne prenant qu'un sommet sur deux de l'hypercube ; 8 des 16 cellules de l'hyperoctaèdre sont alors les demi-cellules de l'hypercube. |
 |
 |
Voir aussi l'hyperoctaèdre
de dimension quelconque.
| polyèdre suivant | polyèdre précédent | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2010