TRIAKI-TÉTRAÈDRE
Triakis tetrahedron, Triakistetraeder
| polyèdre suivant | polyèdre précédent | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
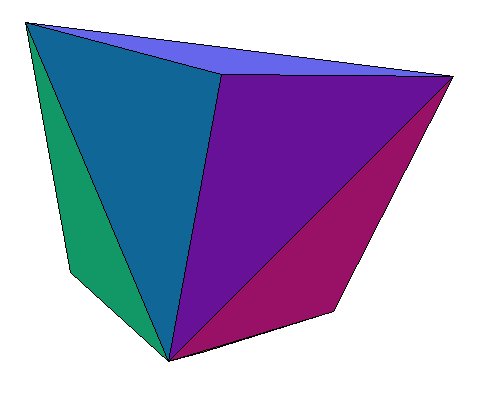
TRIAKI-TÉTRAÈDRE
Triakis tetrahedron, Triakistetraeder

| Famille | polyèdre semi-régulier de deuxième espèce ou polyèdre de Catalan |
| Historique | étudié par Catalan en 1862 |
| Etymologie | du grec "triakis" trois fois et tétraèdre |
| Autres noms | tritétraèdre, tétraèdre trigonal, tétraèdre à toits |
| Dual | tétraèdre tronqué |
| Faces | 12 triangles isocèles d'angle au sommet 2.arcsin
5/6 = 112° 53', de code de Schläfli
3.62
le triaki-tétraèdre est donc un dodécaèdre |
| Sommets | 4 sommets de degré 3, de code de Schläfli 33, et 4 de degré 6 de code 36 |
| Arêtes | 6 arêtes de longueur |
| Patron et graphe |
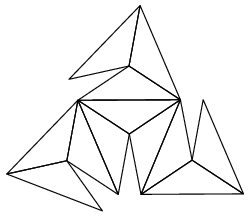 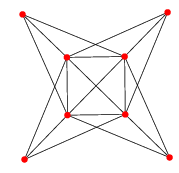 |
| Diamètres | sphère inscrite : |
| Mensurations | volume : coefficient isopérimétrique : |
| Constructions | Dual polaire du
tétraèdre
tronqué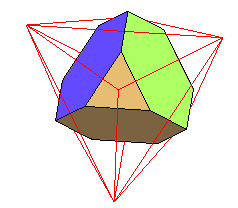
Tétraèdre régulier augmenté de 4 pyramides droites dont la hauteur ( 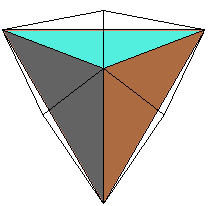 |
| Coordonnées
des sommets |
sommets du tétraèdre : sommets des pyramides : |
| Groupe des isométries | = celui du tétraèdre. |
| polyèdre suivant | polyèdre précédent | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2014