Polyèdres de Catalan étudiés par icelui en 1862, et pavages de Laves étudiés par icelui en 1932. Eugène Charles Catalan (1814-1894) : mathématicien franco-belge. Fritz Laves (1906-1978) : chimiste allemand. voir en.wikipedia.org/wiki/List_of_convex_uniform_tilings

Les polyèdres de Catalan sont les 13 polyèdres semi-réguliers de deuxième espèce autres que les polyèdres réguliers, les diamants et les antidiamants.
Ce sont les polyèdres duaux des polyèdres d'Archimède.

On peut les caractériser par le code de Schläfli commun aux faces, qui indique, dans l'ordre, les degrés des sommets de chaque face.
Par exemple : 3.5².4 signifie que se succèdent, autour de chaque face, un sommet de degré 3, 2 sommets de degré 5, et un sommet de degré 4.

Un seul possède les symétries du tétraèdre :
 

nom	dual	construction	code de Schläfli	faces	sommets	figure
triaki-tétraèdre	tétraèdre tronqué	tétraèdre augmenté	3.62	12	8

Les autres se répartissent en 2 classes de 6 polyèdres, les premiers ayant les symétries du cube, les seconds celles du dodécaèdre.
 
 

nom	dual	code de Schläfli	construction	figure	nom	dual	code de Schläfli	construction	figure
triaki- octaèdre	cube tronqué	3.82	octaèdre augmenté		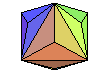triaki-icosaèdre	dodécaèdre tronqué	3.102	icosaèdre augmenté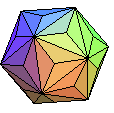
tétraki- hexaèdre	octaèdre tronqué	4.62	cube augmenté		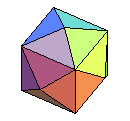pentaki- dodécaèdre	icosaèdre tronqué	5.62	dodécaèdre augmenté
dodécaèdre rhombique	cuboctaèdre	(3.4)2	cube ou octaèdre augmenté		triacontaèdre rhombique	icosidodécaèdre	(3.5)2	dodécaèdre ou icosaèdre augmenté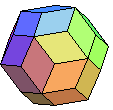
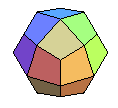
icositétraèdre trapézoïdal	rhombi- cuboctaèdre	3.43	cuboctaèdre augmenté		hexacontaèdre trapézoïdal	rhombicosi-  dodécaèdre	3.4.5.4	icosidodécaèdre augmenté
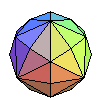
hexaki- octaèdre	cuboctaèdre tronqué	4.6.8	octaèdre ou cube "augmenté"		hexaki- icosaèdre	icosidodécaèdre tronqué	4.6.10	icosaèdre ou dodécaèdre "augmenté"
icositétraèdre pentagonal	cube adouci	34.4			hexacontaèdre pentagonal	dodécaèdre adouci	34.5

Les deux derniers ne sont pas énantiomorphes (c'est-à-dire équivalents à leur image miroir), c'est pourquoi certains comptent 15 polyèdres de Catalan différents au lieu de 13.

Aux 13 polyèdres de Catalan correspondent 13 pavages de la sphère par des polygones sphériques bord à bord, dont le groupe des isométries agit transitivement sur les faces. Nous les relions ci-dessous à 7 des 8 pavages du plan par des polygones réguliers ayant des propriétés similaires, dits pavages "semi-réguliers de deuxième espèce" (dont la définition la plus simple est : pavage polygonal, bord à bord, monoédrique, et tel que tous les angles arrivant à chaque sommet sont égaux).

Tout d'abord, les 5 pavages sphériques obtenus par triangulation centrale des 5 pavages sphériques réguliers (images réalisées par Alain Esculier) :
(on remarquera que les sommets correspondants au polyèdre régulier de départ sont ceux de plus haut degré)
 

triaki-tétraèdre 3.62 (tétraèdre triangulé ; les sommets du tétraèdre sont ceux de degré 4)	triaki-octaèdre 3.82 (octaèdre triangulé ; les sommets de l'octaèdre sont ceux de degré 8)	tétraki-hexaèdre 4.62 (cube triangulé ;  les sommets du cube sont ceux de degré 6)	triaki-icosaèdre 3.102 (icosaèdre triangulé ;  les sommets du tétraèdre sont ceux de degré 15)	pentaki-dodécaèdre 5.62 (dodécaèdre triangulé ;  les sommets du dodécaèdre sont ceux de degré 6)

sont à relier à la triangulation centrale de 2 des 3 pavages réguliers (la triangulation du pavage hexagonal redonnant le pavage triangulaire):

tétraki-quadrillage  4.82 (quadrillage triangulé)	triaki-deltillage  3.122 (deltillage triangulé)

 

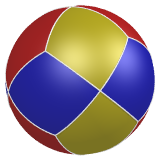
Les deux pavages sphériques obtenus par triangulation centrale et suppression des anciennes arêtes dans un pavage sphérique régulier :			sont à relier au pavage plan obtenu de la même manière
	dodécaèdre rhombique (3.4)2 (triangulation puis suppression des arêtes, partant du cube ou de l'octaèdre)	triacontaèdre rhombique (3.5)2 (triangulation puis suppression des arêtes, partant de l'icosaèdre ou du dodécaèdre)		rhombillage (3.6)2 (triangulation puis suppression des arêtes, partant du pavage hexagonal ou triangulaire)

les deux pavages sphériques obtenus en joignant le centre de chaque face au milieu de chaque arête dans un pavage sphérique régulier :			sont à relier au pavage plan obtenu de la même manière
	icositétraèdre trapézoïdal 3.43 (partant du cube ou de l'octaèdre)	hexacontaèdre trapézoïdal 3.4.5.4 (partant de l'icosaèdre ou du dodécaèdre)		pavage deltoïdal trihexagonal 3.4.6.4, dual du pavage de Diane (partant du pavage hexagonal ou du pavage triangulaire)

les deux pavages sphériques obtenus en joignant le centre de chaque face à chaque sommet et au milieu de chaque arête dans un pavage sphérique régulier :			sont à relier au pavage plan obtenu de la même manière :
	hexaki-octaèdre 4.6.8 (partant du cube ou de l'octaèdre)	hexaki-icosaèdre 4.6.10 (partant de l'icosaèdre ou du dodécaèdre)		kisrhombillage 4.6.12 (partant du pavage hexagonal ou du pavage triangulaire)

 

les deux pavages sphériques duaux des pavages "adoucis"			sont à relier aux 2 pavages plans obtenus par la même méthode :
	icositétraèdre pentagonal 34.4	hexacontaèdre pentagonal 34.5		pentillage du Caire 32.4.3.4	pentillage à fleurs 34.6

Ces 7 pavages sont regroupés sous le nom de "pavages de Laves" ou "de Catalan".

Il existe un huitième pavage semi-régulier de deuxième espèce : , plutôt apparenté aux antidiamants, appelé "pavage pentagonal prismatique".
 
 

Le pavage par des losanges (3.6)2 ci-dessus est très apprécié car le cerveau l'interprète comme un empilement de cubes. La photo ci-contre, tirée de cette page, a été prise près de la cité interdite de Pékin. Photo Lance Belville.

Le pavage pentagonal dit "du Caire" ci-dessus, hormis son côté esthétique, est remarquable par le fait que sa pièce de base est un pentagone à deux angles droits et deux angles de 120°, angles très courants, alors que le pentagone régulier ne peut paver le plan. Un examen précis de la photo ci-contre montre que si la pièce a bien deux angles droits, les 3 autres angles ne sont pas de 120° ; voir plus de détails sur la page spécifique.  Photo Helen Donnelly.

Ci-contre, Détail d'une grille ornant la mosquée Sakirine à Istanboul. On y retrouve la structure du pavage 4.6.12 ci-dessus formé de triangles avec leurs hauteurs.

 
 
 

polyèdre suivant

polyèdre précédent

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL 2015