Quatrefoil

QUATREFOIL CURVE

Other names: four-leaved rose, quadrifolium.

Polar equation: .
Cartesian equation: .
Rational sextic
Cartesian parametrization in a frame turned by : .
Length: .
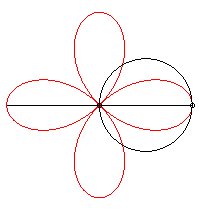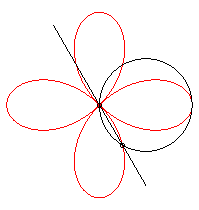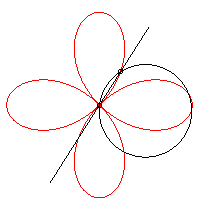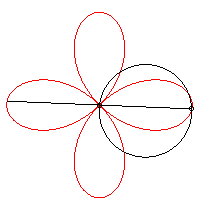
Area: (half of that of the circumscribed disk; the "negative" petals cut on this disk therefore have the same area as the "positive" ones)

The quatrefoil is the rose with four petals.

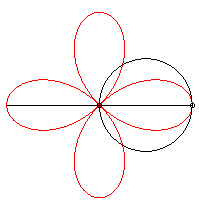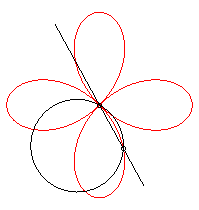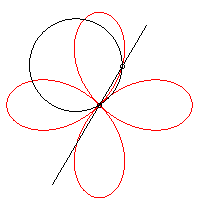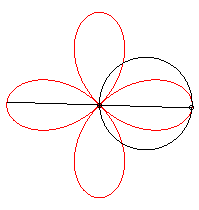
It can be obtained as the trajectory of the second intersection point of a line and a circle turning around one of their points, either in the same direction and the circle going three times as fast as the line, or in opposite directions at the same speed.
It can also be obtained as the trajectory of the second intersection point of two identical circles turning around of of their points, in the opposite direction and one of them going three times as fast as the other:

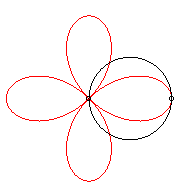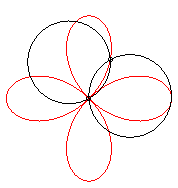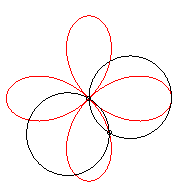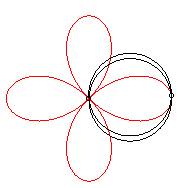The quatrefoil is also:

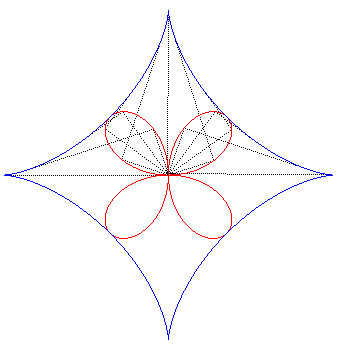    - the locus of the feet of the lines perpendicular at O to a segment line of length 2a the ends of which move on the axes; therefore, it is the pedal with respect to O of the astroid: (the quatrefoil thus is a beetle curve), as well as the envelope of the circles a diameter of which joins O to a point on this astroid.

   - the orthoptic of the astroid.

    - a hypotrochoid:
sum of two circular motions with same radius, opposite directions, angular speeds with ratio 3;
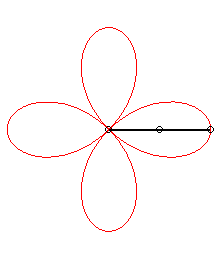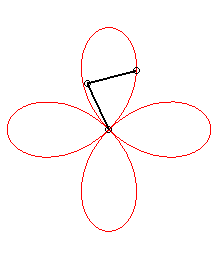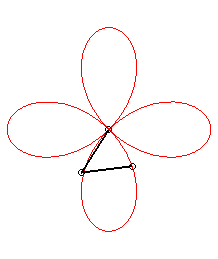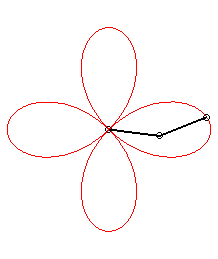or base circle with radius , rolling circle with radius , distance between the point and the rolling circle = .
as the first arm completes one turn, the second one completes 3 turns.

It can also be obtained as an orthopolar of a circle.

Like all roses, the quadrifolium is a view from above of a clelia. This elegant spherical curve with cylindric equation is here a limit case of the seam line of a tennis ball.

The quadrifolium can also be obtained by projections based on a cylindric sine wave with 2 arches (or pancake curve), through a 3D basin.

Opposite, homothetic quadrifolia (in red), and their orthogonal trajectories.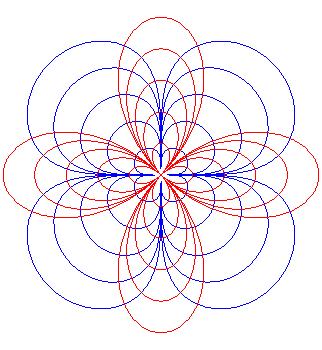

Here are a few variations providing slightly more realistic quatrefoils:

Reunion of two
lemniscates of Bernoulli

Two quadrifolia with asymptotes: , i.e. (decic),
and , i.e. (octic).

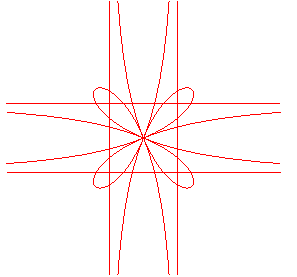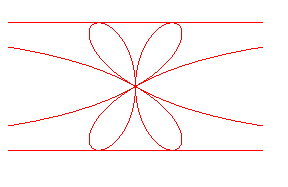See also Ceva trisectrix, double egg, conical rose, and Enneper surface.

Superb quadrifolium traced by a poi player.
Three loops of a quadrifolium located on 3 orthogonal planes constitute the edge of a three-blade helix, the projection of which is a (false) regular trifolium...
See also the self-intersection curve of the Boy's surface.

next curve previous curve 2D curves 3D curves surfaces fractals polyhedra

- the locus of the feet of the lines perpendicular at O to a segment line of length 2a the ends of which move on the axes; therefore, it is the pedal with respect to O of the astroid: (the quatrefoil thus is a beetle curve), as well as the envelope of the circles a diameter of which joins O to a point on this astroid.
- the orthoptic of the astroid.
- a hypotrochoid: sum of two circular motions with same radius, opposite directions, angular speeds with ratio 3; or base circle with radius , rolling circle with radius , distance between the point and the rolling circle = .	as the first arm completes one turn, the second one completes 3 turns.