En notant la colatitude, équation sphérique : , l’axe étant Oz et le demi-angle au sommet . Équation cylindrique :  . Équation cartésienne : . . Paramétrisation cartésienne :   (). Paramétrisation à partir des coordonnées polaires  du plan de développement : . Première forme quadratique fondamentale : . Elément d'aire : . Deuxième forme quadratique fondamentale :   ; . Rayons de courbures principaux :  ; tous les points sont paraboliques. Le cône droit de directrices Ox et Oy et d'axe la droite y = x, z = 0 a pour équation cartésienne : ; Le cône de directrices Ox Oy et Oz et d'axe la droite x = y = z a pour équation cartésienne : xy + yz + zx = 0 (l'angle au sommet vaut arccos (-1/3) » 109 ° 28 ') Volume d'un tronc de cône limité par un sommet, de base de rayon R et de hauteur h :  Aire correspondante : .

Autre paramétrisation :  (les lignes de coordonnées sont des courbes de Viviani).
Volume du tronc de cône limité par les plans  et  :  ; voir à neiloïde.

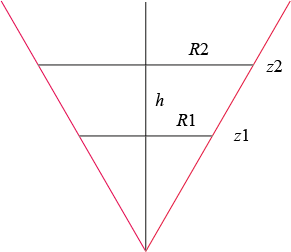On peut développer le cône en faisant correspondre à un point M du cône le point du plan de coordonnées polaires  ; un demi-cône devient alors un secteur angulaire d’angle . En particulier le demi-cône de demi-angle au sommet  ci-contre se développe en un demi-plan.

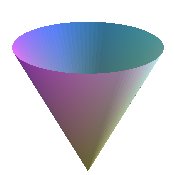Courbes remarquables tracées sur le cône de révolution :
 

- à tout seigneur, tout honneur : les sections planes ou coniques : ellipses, paraboles et hyperboles. Elles se développent en les polygastéroïdes d'indice n >1. La coupe par le plan  donne une ellipse, une parabole, ou une hyperbole, suivant que  est supérieur, égal ou inférieur à  ; si l'on roule le cône sur un plan, elle se développe en la polygastéroïde d'équation polaire : . Ci-contre, le cas , avec la polygastéroïde développée.
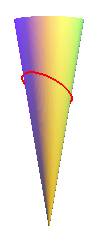- les lignes de courbure, qui sont les parallèles (cercles) et les méridiennes (droites)
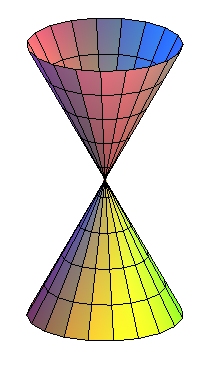- les géodésiques, qui sont les courbes qui se développent en des droites ; il y a les génératrices et les courbes d’équation sphérique :  , qui se développent en les droites . Ce sont les relèvements sur le cône des épis du plan xOy d'équation : .
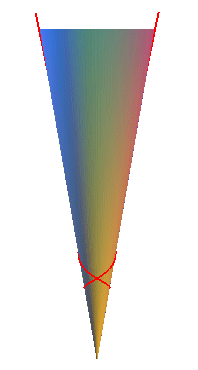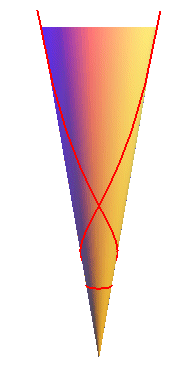- les cercles géodésiques, qui se développent en des cercles.  Équation sphérique dans le cas des cercles passant par O :  ; ils se développent en les cercles . Ce sont les relèvements sur le cône des rosaces du plan xOy d'équation : .
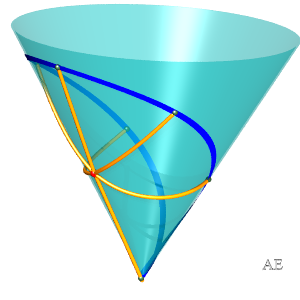- les hélices, qui sont aussi les loxodromies ; ce sont des relèvements de spirales logarithmiques : voir hélice conique.
- les spirales coniques de Pappus, relèvements de spirales d'Archimède.
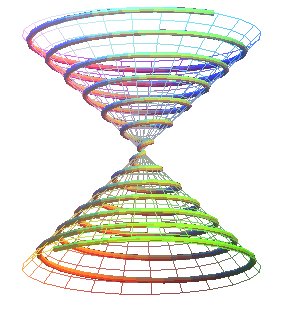- les spirales coniques hyperboliques.
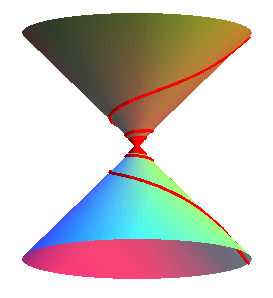- les rosaces coniques, dont la courbe de Viviani.
- les chaînettes coniques.

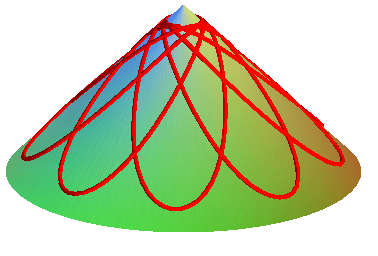Voir aussi les cycloïdes sphériques, lieux d'un point d'un cone de révolution roulant sans glisser sur un autre cone de révolution, ainsi que les ovales de Descartes, projections de l'intersection de deux cônes de révolution d'axes parallèles.

Des cônes dans la nature :
 

Et ailleurs :
 

surface suivante

surface précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL 2018