Courbe étudiée par Dioclès, 180 av. J.C. ; Fermat ; Huygens. Du grec Kissos : lierre, en lien probablement avec les nervures...  Dioclès (IIème siècle av. J.C.) : mathématicien grec.

Équation polaire :  . Équation cartésienne :   (la courbe  est étudiée ici).  Cubique circulaire rationnelle à point de rebroussement. Paramétrisation cartésienne rationnelle : , soit  (avec t = tanq). Angle tangentiel cartésien :  . Abscisse curviligne : , . Rayon de courbure : . Aire entre la courbe et son asymptote :  .

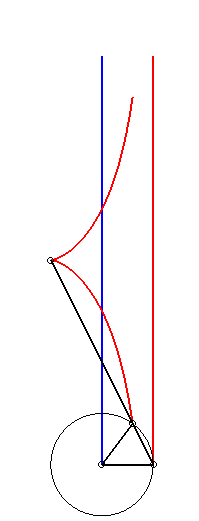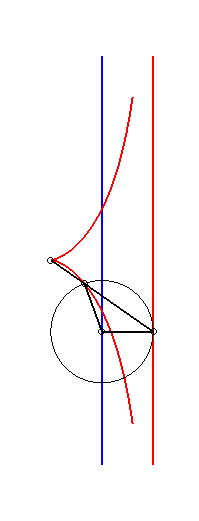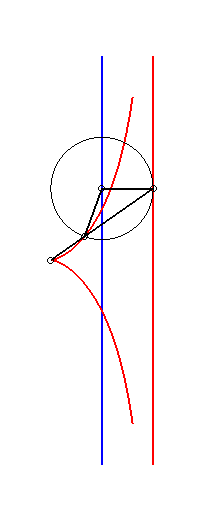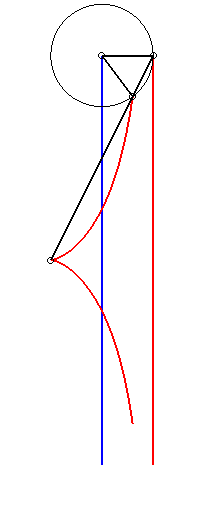
La construction la plus simple de la cissoïde droite se fait par double projection sur 2 droites parallèles : étant donnés deux droites parallèles (T) et (T ') et un point O de (T '), un point variable P de (T) se projette en Q sur (T'), lequel se projette en M sur (OP) : la cissoïde droite est le lieu de M.

Comme toute cubique circulaire rationnelle, la cissoïde de Dioclès peut être définie comme :
 

- la cissoïdale de pôle O d’un cercle de diamètre [OA] et de la tangente en A au cercle (ici A(–a,0))...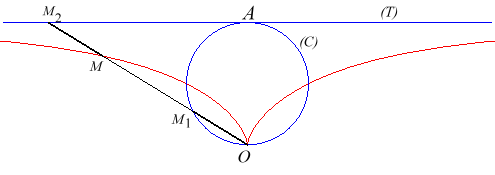
... et donc aussi comme médiane de cercle et droite.
- la podaire d’une parabole par rapport à son sommet (ici la parabole de sommet O et de foyer F, symétrique de A par rapport à O)...
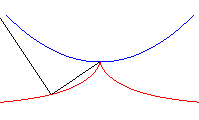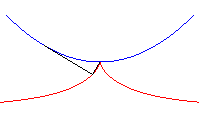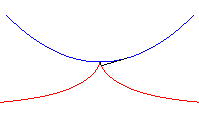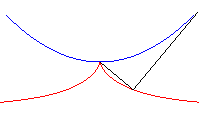... et donc aussi comme comme enveloppe des cercles centrés sur une parabole et passant par son sommet.
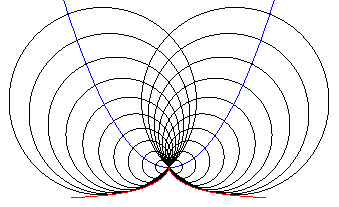- l’inverse d’une parabole par rapport à son sommet (ici la parabole de sommet O et de foyer A, le cercle d'inversion étant le cercle de centre O passant par A).

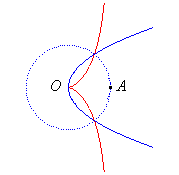Comme toute cubique circulaire rationnelle droite, la cissoïde droite se construit...
 

...par la méthode de l'équerre de Newton :	...comme kiéroïde

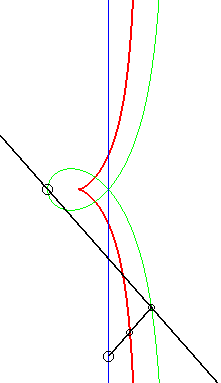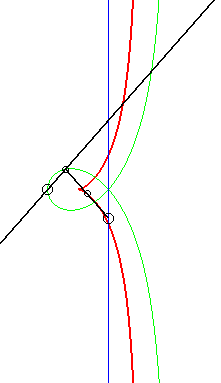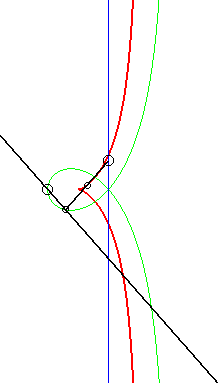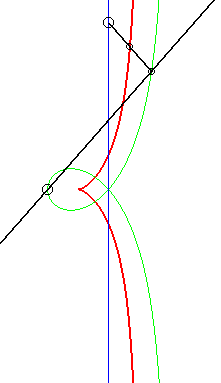Elle peut encore être définie comme :
 

- le lieu du sommet d’une parabole roulant sans glisser sur une parabole isométrique, les deux paraboles étant extérieures l’une à l’autre, et les sommets venant en contact (voir à orthotomique).
-  le lieu du foyer d'une parabole variable de sommet fixé et passant par un point fixé (voir à glissette).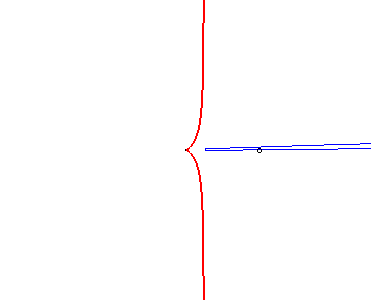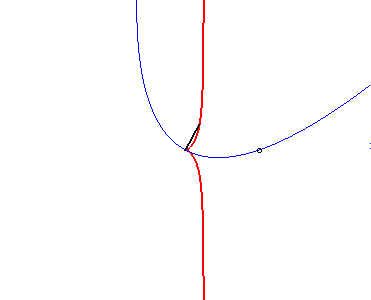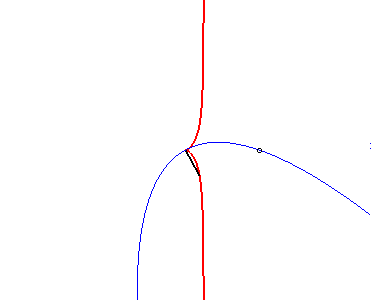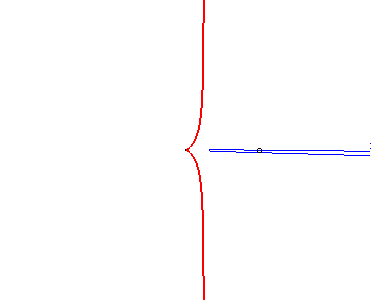
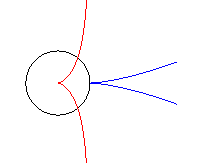
- l’orthocaustique d'une cardioïde par rapport à son sommet (ici, cardioïde de point de rebroussement (a, 0) et de sommet (4a, 0)).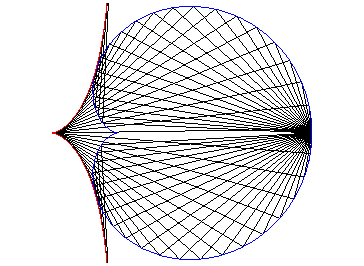
- courbe de Rosillo : un diamètre [BC] d'un cercle étant donné, et un point P décrivant ce cercle, la cissoïde est le lieu du point d'intersection de la perpendiculaire à [BC] passant par P et de la parallèle à (CP) passant par B.

Elle est enfin également un cas particulier d'hyperbole cubique et d'ophiuride.
 

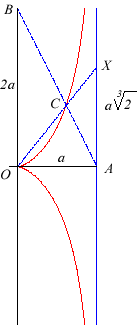La cissoïde de Dioclès est une duplicatrice : si B est le point de coordonnées (0, 2a) et C le point d'intersection de (C) avec (AB), les coordonnées du point X d'intersection de (OC) avec (T) sont (a,  ).

 

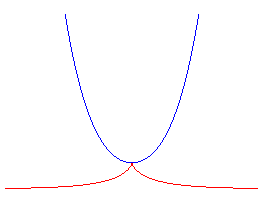La développée de la cissoïde droite est la quartique polynomiale . Figure à ne pas confondre avec celle formée de la tractrice et de sa développée la chaînette.

Sa polaire par rapport au cercle de centre O et de rayon a est une parabole semi-cubique : .

 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL, Jacques MANDONNET 2010