
serpentine droite 2
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
CUBIQUE CIRCULAIRE FOCALE
Focal
circular cubic, Fokalkreiskubik
| cas oblique | cas droit | |
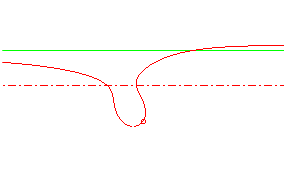
| focale à branche unique |
 |
 |
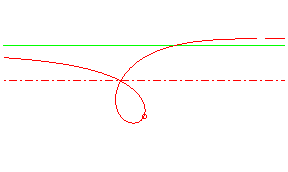
| focale à noeud (strophoïde) |
 |
 |
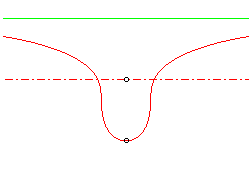
| focale à ovale |
 |
 |
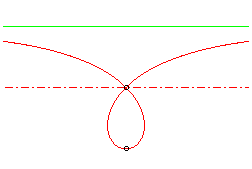
| cas où le foyer est sur l'axe |
 |

serpentine droite 2 |
| Courbe étudiée par Van Rees en 1829, Steiner
en 1852 et Laguerre en 1868.
Autres nom : focale de Van Rees, cubique isoptique, cubique d'Apollonius, cubique circulaire axée (appellation donnée en 2002 par Dominique Roux et Michel Tixier). Références : [Brocard Lemoyne] III, p. 92 à 100 ; [Gomes Texeira] I, p. 45 à 58. |
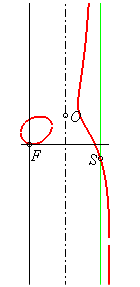 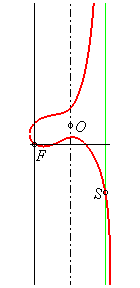 |
L'origine du repère étant placée
au foyer singulier F :
Équation cartésienne : l'axe est x = a, l'asymptote x = 2a, O(a, a tan a) et le point d'intersection avec l'asymptote S( 2a, - 2a cot 2a). Cubique circulaire. Équation complexe : Équation polaire : |
Les cubiques circulaires focales, ou focales tout court, sont les cubiques circulaires contenant leur foyer singulier F (point d'intersection des tangentes aux points cycliques) ; autrement dit, les points cycliques ont le même tangentiel (i.e. point où la tangente recoupe la courbe). En prenant pour foyer le centre du repère et pour asymptote la droite x = 2a, on obtient l'équation réduite ci-dessus.
La cubique est elliptique
si , à
ovale si
,
à une branche si
,
et rationnelle
si
, auquel
cas on retrouve les strophoïdes.
L'équation complexe ci-dessus montre que les cubiques
circulaires focales sont les lieux des points M tels que l'image
M'
par une composée d'inversion de centre F avec une réflexion
d'axe passant par F soit telle que le milieu de [MM'] décrive
une droite D. Cette droite est appelée l'axe de la
focale (d'où l'appellation cubique circulaire axée).
Les points M et M' sont dits conjugués
et se construisent très simplement l'un par rapport à l'autre
par le fait qu'ils ont le même tangentiel.
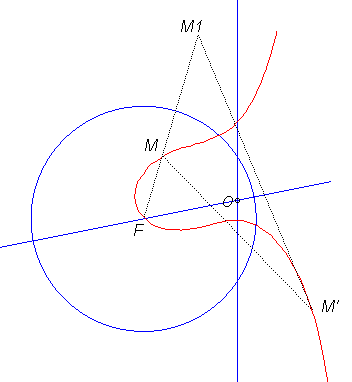 |
M1 est
l'inverse de pôle F de M par rapport au cercle bleu
et M' le symétrique de M par rapport à (OF).
Le milieu de [M M'] décrit l'axe de la focale. Les tangentes en M et M' se coupent en un point de la focale. |
La cubique possède un axe de symétrie lorsque
la réflexion ci-dessus a un axe perpendiculaire à l'axe de
la focale, auquel cas elle est dite droite (ici, l'axe de symétrie
est
Ox, obtenu pour
= 0), ou lorsque le foyer se trouve sur son axe, qui est alors aussi l'asymptote
(ici, l'axe de symétrie est
Oy, obtenu pour a =
0) ;
Lorsqu'on n'est pas dans ce dernier cas, la construction
géométrique la plus simple des focales se fait comme lieu
des points de contact des tangentes issues d'un point (le foyer) aux cercles
d'un faisceau de cercles. L'axe radical du faisceau est l'axe de la focale.
Lorsque
le faisceau est à points de base (à gauche ci-dessous), on
obtient les focales à une branche, lorsqu'il est à points
de Poncelet, les focales à ovale, et lorsqu'il est singulier, les
strophoïdes ; le centre du faisceau est .
La focale est aussi le lieu des intersections des droites
issues de F avec les cercles du faisceau orthogonal au précédent
centrés sur ces droites.
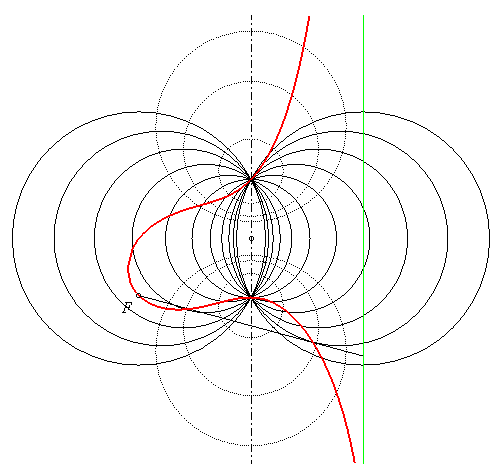
Les points de contact des tangentes aux cercles du premier faisceau issues de F décrivent la focale ; le faisceau orthogonal est en pointillé. Les deux points de base du premier faisceau (points de Poncelet du deuxième) sont les les points d'intersection de la focale avec son axe. |
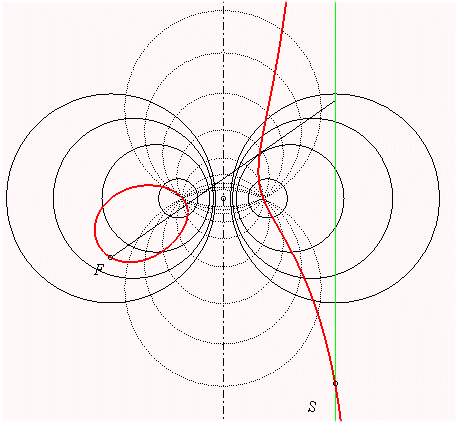
Les points de contact des tangentes aux cercles du premier faisceau issues de F décrivent la focale ; le faisceau orthogonal est en pointillé. Les deux points de Poncelet du premier faisceau (points de base du deuxième) sont les projetés de F sur la courbe. |
Toujours pour a > 0, Les focales possèdent également une élégante construction en 3D découverte par Van Rees, comme lieu des foyers de coniques.
a) Dans le cas non droit (
différent de 0).
Si S est le point d'intersection de la focale avec
son asymptote et O', le point d'intersection de la bissectrice de
FSy
avec l'axe, F' le symétrique de F par rapport à
O'
(situé sur l'asymptote) et (C) le cône elliptique de
sommet S et de directrice l'ellipse orthogonale au plan de la focale
de demi-axes
et b, la focale est le lieu des foyers des coniques sections du
cône (C) avec les plans perpendiculaires au plan (OSF)
passant par F.
On obtient une focale à ovale lorsque FF'
est le grand axe de l'ellipse directrice, une focale à une branche
quand c'est le petit axe, et une strophoïde quand cette ellipse est
un cercle.
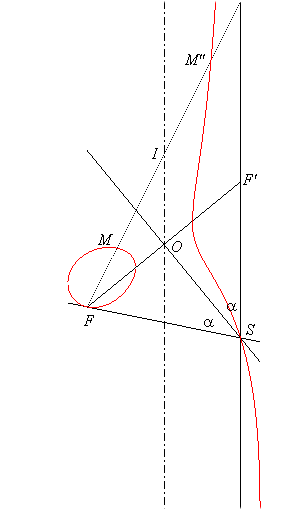 |
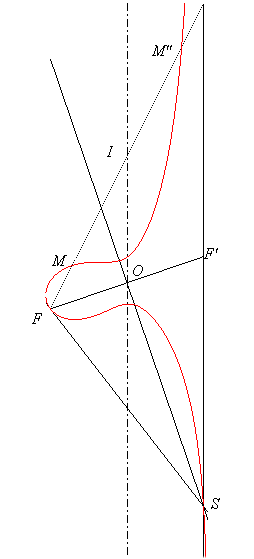 |
S, sommet du cône, M et M" : foyers de la conique section du cône par un plan perpendiculaire à (OSF) passant par F ; le centre I de la conique décrit l'axe de la focale. |
b) Dans le cas droit (
= 0).
Si (C) est le cylindre elliptique d'axe l'axe de
la focale et de directrice l'ellipse orthogonale au plan de la focale de
demi-axes
OF = a et b, la focale est le lieu des foyers des
coniques sections du cylindre (C) avec les plans perpendiculaires
au plan de la focale passant par F.
On obtient une focale à ovale lorsque FF'
est le grand axe de l'ellipse directrice, une focale à une branche
quand c'est le petit axe, et la strophoïde de Newton quand cette ellipse
est un cercle.
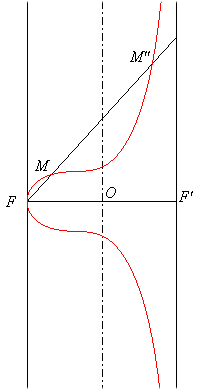 |
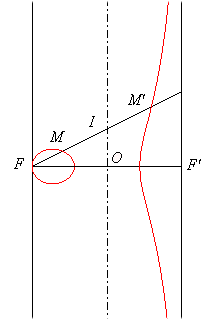 |
M et M'' : foyers de la conique section du cylindre par un plan perpendiculaire au plan de la focale passant par F ; le centre I de la conique décrit l'axe de la focale. |
Interprétation comme cubique isoptique.
| Étant donnés deux points A et B
d'une
focale, et les deux conjugués A' et B', la focale
associée est le lieu des points M d'où les segments
orientés
[AB]
et [B'A'] sont vus sous le même angle (i. e. les angles de
droites (MA, MB) et (MB', MA') sont égaux),
d'où le nom de cubiques
isoptiques
aussi donné aux focales.
Réciproquement, étant donnés deux
segments orientés [AB] et [B'A'] dans le plan, le
lieu des points d'où l'on voit ces deux segments sous le même
angle est en général une focale.
|
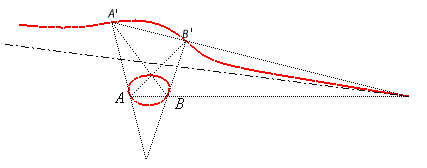
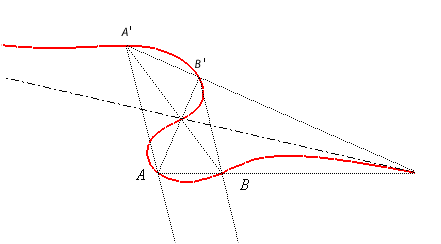 |
| Animation de cette construction. | 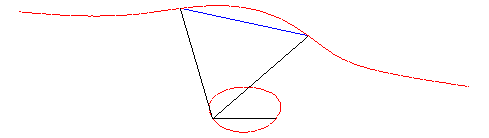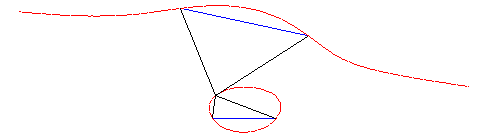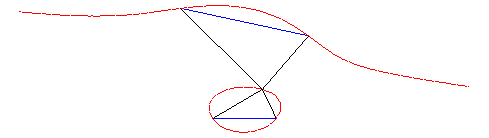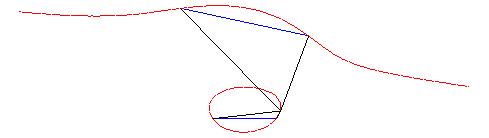 |
 |
4 points A,B,C,D tels que les 6 droites les joignants
soient 2 à 2 sécantes définissent 3 focales :
La focale rouge est le lieu des points M tels que (MA,MB) = (MC, MD), ou (MA, MC) = (MB, MD) ; elle passe donc par le point d'intersection de (AB) et (CD) et celui de (AC) et (BD). La focale bleue est le lieu des points M tels que (MA, MC) = (MD, MB) ou (MA, MD) = (MC, MB) ; elle passe donc par le point d'intersection de (AC) et (BD) et celui de (AD) et (BC). La focale verte est le lieu des points M tels que (MA, MD) = (MB, MC) ou (MA, MB) = (MD, MC) ; elle passe par le point d'intersection de (AD) et (BC) et celui de (AB) et (CD). |
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2016