Courbe étudiée par Barrow (l'un des professeurs de Newton) en 1669, par Quételet en 1810 et par Chasles ; le nom a été donné par Enrico Montucci en 1837. Strophoïde vient du grec strophos « cordon, ceinture, torsade ».  Autres noms : focale de Quételet, focale à noeud, courbe harmonique.

 

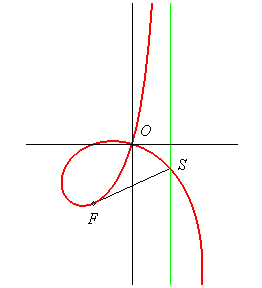La tangente au foyer F recoupe la courbe au point d'intersection S avec l'asymptote.

Équation polaire : avec  ;  .  = 0 : strophoïde droite ;  = p/2 : cas limite du cercle . Foyer F  ; asymptote : x = a cos ;  Point d'intersection avec l'asymptote : S. Point d'inflexion obtenu pour . Équation cartésienne : . Cubique circulaire rationnelle à point double. Dans le repère (F , ) : Équation cartésienne : . Équation complexe : , avec . Équation polaire : ,  soit , le cas + donnant la même courbe que le cas -. Si l'on échange et , l'équation polaire se simplifie en :  (donc conchoïde de strophoïde droite).

 

Deux points O et F et une droite (D0) passant par O étant donnés, la strophoïde de foyer F, de point double O et d'axe (D0) est le lieu des points M d'une droite variable (D) passant par F tels que PM = PO où P est le point d'intersection de la droite (D) avec (D0) (autrement dit, c’est la strophoïdale de (D0) relativement à O et F).	La strophoïde est le lieu des points M tels que PM = PO
La strophoïde est donc aussi le lieu des points de contact des tangentes issues de F aux cercles tangents en O à l'axe (D0).

Il résulte de cette définition que l'axe (D₀) de la strophoïde est la courbe médiane de pôle O de la strophoïde avec elle-même.

Ici, O est l’origine du repère, F est le point , et (D₀) est l’axe Oy ; l’asymptote est la droite parallèle à (D₀) passant par le symétrique de F par rapport à (D₀).
 
 

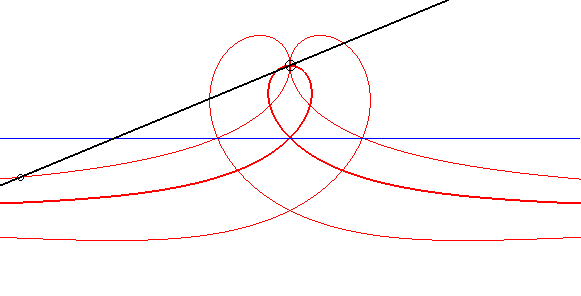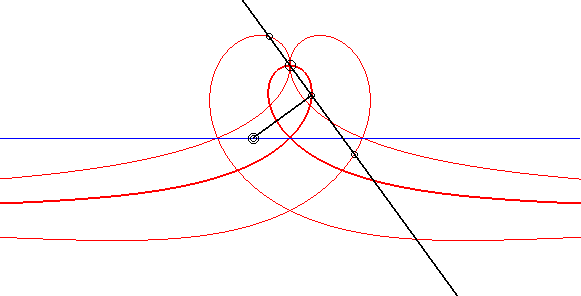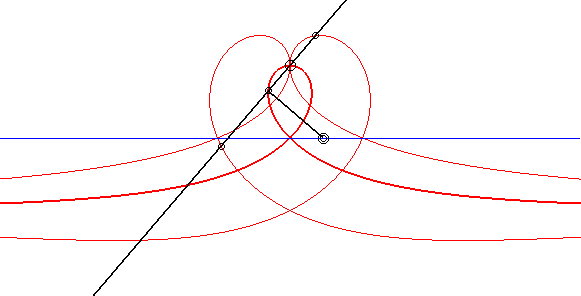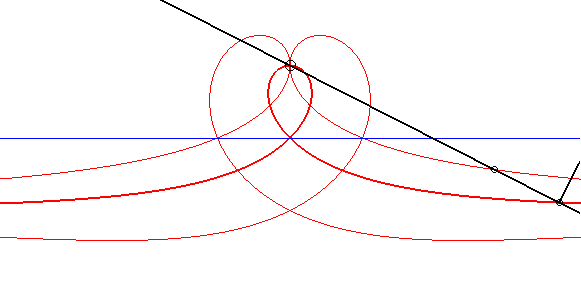
Animation montrant la construction de la strophoïde droite par l'équerre de Newton, et deux strophoïdes conchoïdes. Voir des détails sur la page des glissettes.

L'équation complexe montre que les strophoïdes sont les lieux des points M tels que l'image M' par une composée d'inversion de centre F avec une réflexion d'axe (OF) soit telle que le milieu de MM' décrive une droite (D₀) passant par O ; M' est appelé le conjugué de M.
 

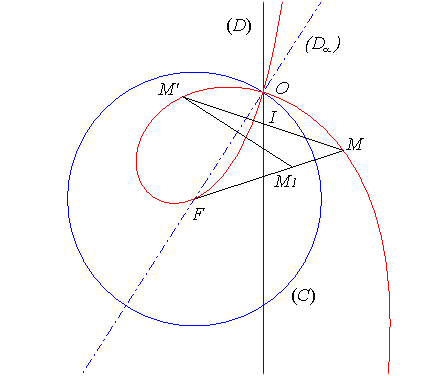Le milieu I de [M M'] décrit la droite (D0) ; M1 est l'inverse de pôle F de M par rapport au cercle (C) et M' le symétrique de M1 par rapport à (Da ).

Si A et A' sont deux points conjugués de la strophoïde, et M un point quelconque de cette courbe, la droite (OM) est bissectrice de (AMA') ; inversement, étant donnés 3 points non alignés O, A, A' le lieu des points M tels que (OM) est bissectrice de (AMA') est une strophoïde, ou, ce qui revient au même, le lieu des points M "voyant" les segments orientés [AO] et [OA'] sous le même angle.
La strophoïde est donc un cas particulier de cubique isoptique, lieux des points d'où l'on voit deux segments sous le même angle.
 

Un triangle non aplati (ABC) donne donc naissance à 3 strophoïdes : (SA) définie par (MC, MA) = (MA, MB) en mauve (SB) définie par (MA, MB) = (MB, MC) en brun (SC) définie par (MB, MC) = (MC, MA) en vert Lorsque le triangle est aplati, ces lieux sont des cercles dits d'Apollonius, d'où le nom de strophoïdes d'Apollonius données à ces courbes. Les trois courbes, ont, en général, 5 points communs : les 3 sommets, le point de Fermat du triangle F1 , défini par  si (ABC) est de sens direct, et le deuxième point de Fermat F2  défini par . F1 et F2 sont les deux centres isogonaux du triangle. Chaque courbe passe aussi par le pied de la hauteur issue du point en indice.

 
 

La strophoïde se retrouve aussi dans le problème d'optique suivant : un observateur B regarde l'image A' d'un point fixe A dans un miroir tournant autour d'un point fixe O; le lieu du point d'intersection du rayon BA' avec le miroir est une strophoïde de point double O, de foyer A, d'axe parallèle à (BE) construit sur la figure. Si D est le symétrique de A par rapport à OB, la droite (BD) est la tangente en B.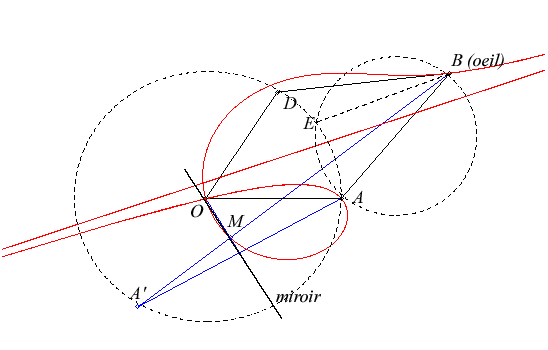

Les strophoïdes possèdent encore une élégante construction en 3D découverte par Quételet, comme lieu des foyers de coniques (d'où l'appellation : focale de Quételet) : si S est le point d'intersection de la strophoïde avec son asymptote et (C) le cône de révolution d'axe (OS) passant par F (de demi-angle au sommet), la strophoïde est le lieu des foyers des coniques sections du cône (C) avec les plans perpendiculaires au plan (OSF) passant par F.
 

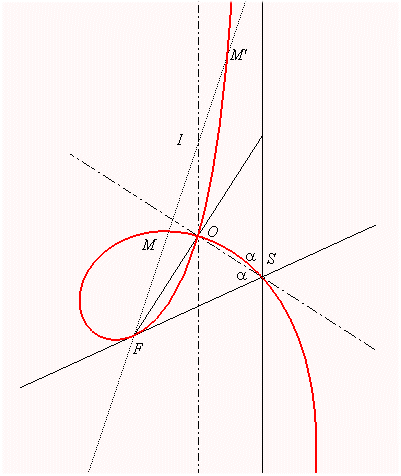S, sommet du cône, M et M' : foyers de la conique d'un plan perpendiculaire à (OSF) passant par F ; le centre I de la conique décrit l'axe de la strophoïde.   Pour la strophoïde droite, le cône devient un cylindre.

Comme toutes les cubiques circulaires rationnelles, les strophoïdes peuvent être définies comme :

     - les cissoïdales de pôle O d’un cercle passant par O et d’une droite passant par le symétrique du centre du cercle par rapport à O (ici le cercle est le cercle (C) de centre F passant par O, la droite, la droite parallèle à (D₀) passant par le symétrique de F par rapport à O).

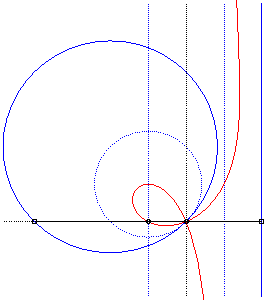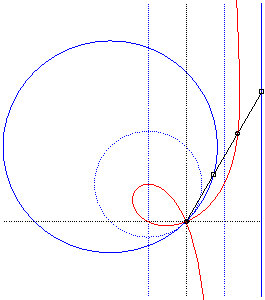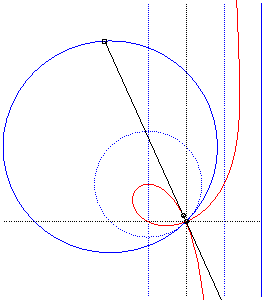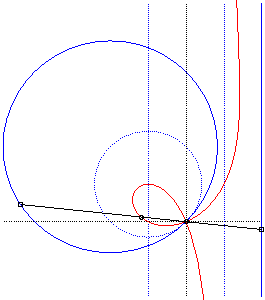
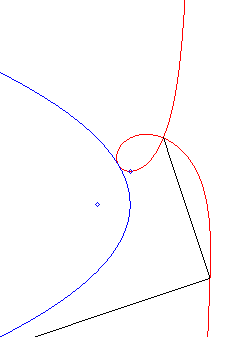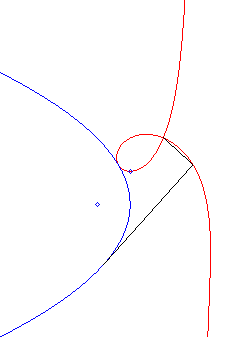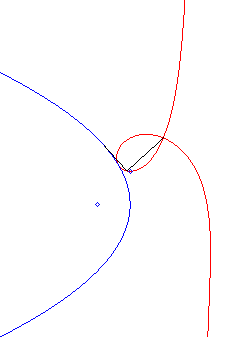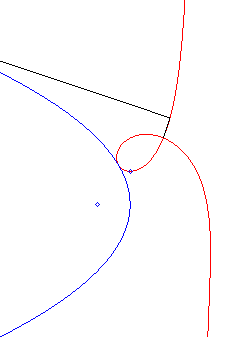Le foyer de la strophoïde est au milieu du segment joignant son point double au foyer de la parabole. La strophoïde est donc aussi l'enveloppe des cercles de diamètre joignant O et un point de la parabole ; autrement dit c'est une cyclique de déférente une parabole, avec une puissance d'inversion nulle et un pôle sur la directrice de la parabole.

 - les inverses d’une hyperbole équilatère par rapport à un de ses points (ici O)

Voir à cochléoïde et à surface de Möbius.
 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL, Jacques MANDONNET 2016