Poisson : nom maison.

 

Forme 1 Paramétrisation cartésienne : . Équation cartésienne : . Quartique rationnelle.
Forme 2 (image par une rotation d'angle  amenant le point double en O ) Équation cartésienne :  avec  et .

 

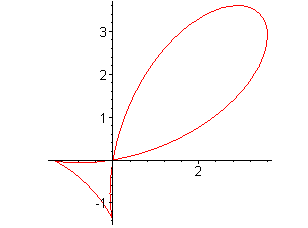Les "poissons" sont les projections sur les plans passant par l'axe Oy de la courbe de Viviani : .

 

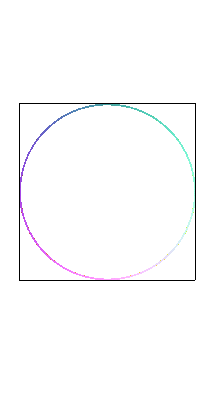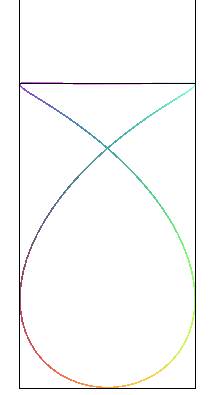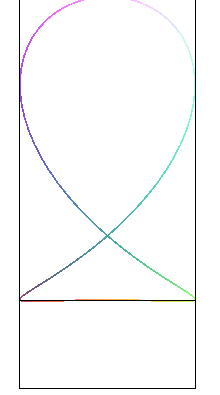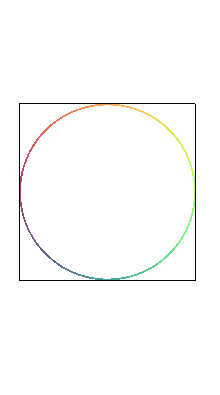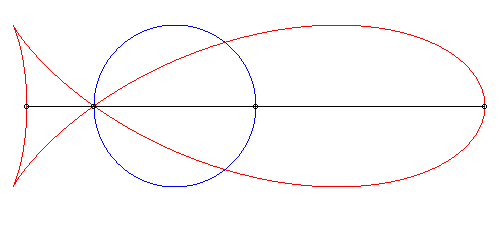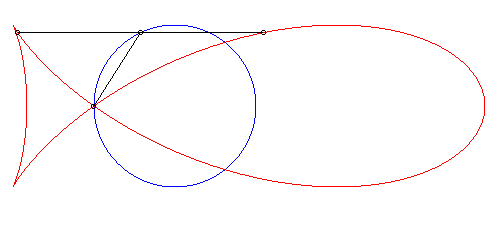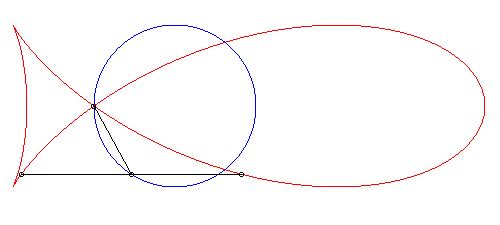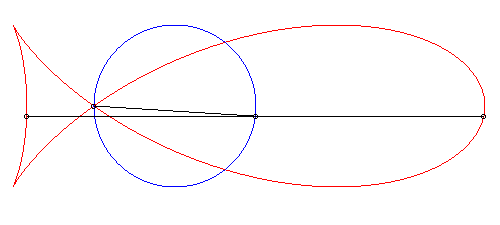
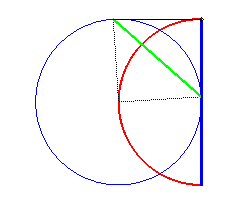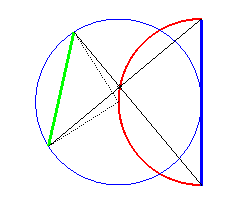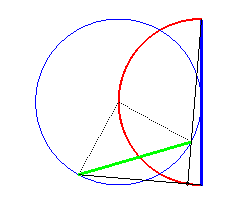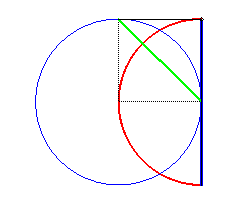
Etant donné un cercle (C), un point fixe O de ce cercle, un point N variable de ce cercle et la droite (D) parallèle au diamètre passant par O, le "poisson" de paramètre k est le lieu des points d'intersection du cercle de centre N et de rayon kON avec la droite (D). Cette constrution est une généralisation de la construction strophoïdale (cas où k = 1).

Dans le cas k = 2, soit q = 0, on obtient la torpille.
Remarque : dans ce dernier cas, si l'on échange dans la paramétrisation les fonctions sin et cos, on obtient le bifolium régulier.
 

Pour 0 < k < 2, soit 0 < q < 1, le "poisson" possède 3 points singuliers formant un triangle rectangle isocèle : A = (0, 0), B = (qa, 0), C = (0, qb) (repère de la forme 2) permettant l'interprétation géométrique suivante : le poisson est la solution de la recherche du lieu des points M tels que le rapport de l'aire algébrique du triangle (ABC) à celle du triangle (A'B'C') est égale à q/(1 – q), où A' B', C' sont les centres des cercles cisconscrits à (MBC), (MCA), (MAB) [François Duc, 2011]. Les points B et C sont des points de rebroussement ssi , soit q = –1, et la courbe prend alors une forme de poisson à nageoire arrière pointue.

 

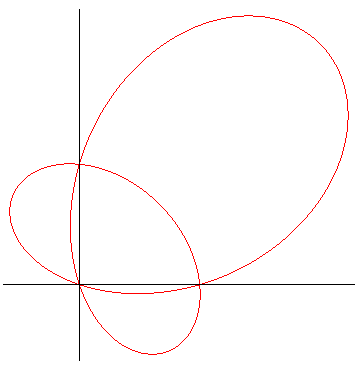Les "poissons" peuvent aussi s'obtenir par la construction suivante (cf. la courbe de superposition navale) : étant donné un segment fixe [AB] de longueur 2L situé à une distance L du centre d'un cercle de rayon R, et une corde  [PQ] d'angle au centre p/2 du cercle, les vecteurs AB et PQ ayant même sens quand ils sont le plus éloignés,  le poisson est le lieu des points d'intersection des droites (AP) et (BQ). La relation entre a,b,L,R est  ; on obtient le poisson à nageoire pointue pour L=R.

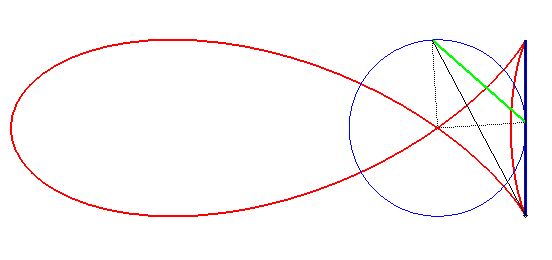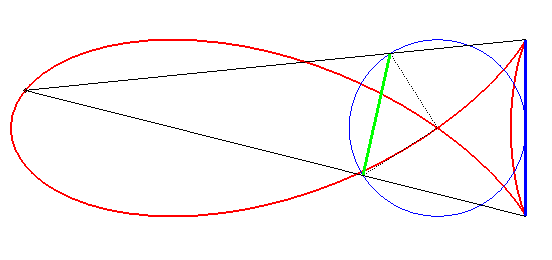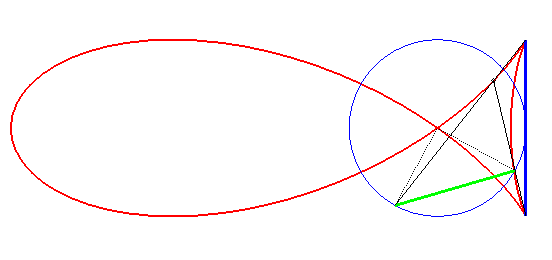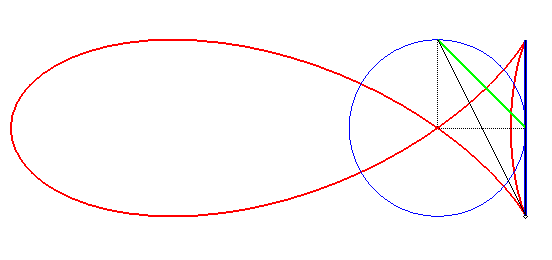Si on échange P et Q on obtient un simple arc de cercle :

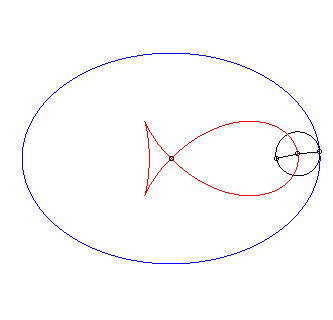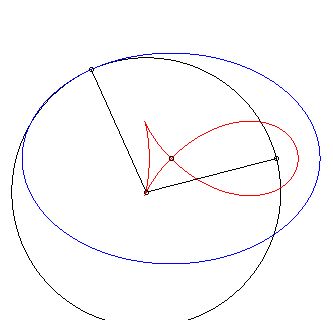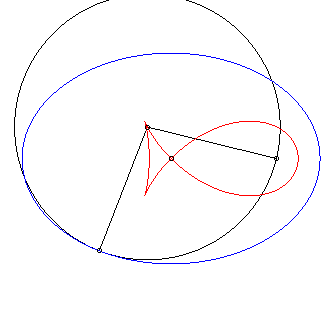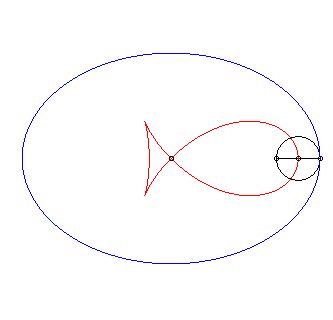
Le "poisson à nageoires pointues" est, à dilatation près, l'antipodaire d'une ellipse d'excentricité  par rapport à son foyer, donc aussi, comme le montre l'animation ci-contre, le lieu des points équidistants de l'ellipse et du foyer.

Variante pour des poissons siamois :.

© Robert FERRÉOL  2015