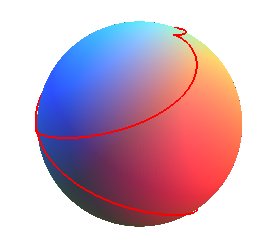
cas q = 5/2, k » 0,56, pente » 75%

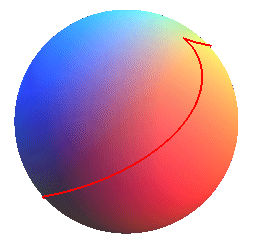
cas q = 2/5, k » 0,17, pente » 25%

 

Voir Loria 3d p. 84 et 160.

Paramétrisation cartésienne :  soit  avec , , .

Les hélices sphériques sont les hélices, autrement dit les courbes de pente constante par rapport à un plan P donné, tracées sur une sphère.

On démontre que ce sont les courbes décrites par un point d'un grand cercle de la sphère roulant sans glisser sur un cercle fixe de cette sphère, parallèle au plan P ; ce sont donc des cas particuliers de cycloïdes sphériques ; elles possèdent des points de rebroussement situés sur le cercle fixe et son symétrique par rapport au centre de la sphère.

Ici R est le rayon de la sphère, O son centre, r = k R le rayon du cercle fixe ; la pente constante est .

La deuxième paramétrisation ci-dessus montre que les projections sur le plan du cercle fixe sont des épicycloïdes de paramètre q défini par .

Les hélices sphériques sont aussi les développantes de cône de révolution (lieux d'un point d'un plan roulant sans glisser sur le cone) ; l'hélice ci-dessus est une développante du cône de révolution passant par les deux cercles de roulement.

Ne pas confondre ces courbes avec les loxodromies, dont les tangentes font un angle constant, non avec un plan, mais avec les méridiens, ni avec les clélies.

Hélice sphérique de pente 10%0 ; elle ressemble à une loxodromie, mais contrairement à celles-ci, les points extrêmes ne sont pas des points asymptotes.

Modèle d'hélice sphérique obtenue comme développante de cône, tiré de ce site.

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL  2006