

| surface suivante | surface précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
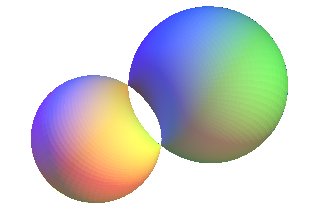
CYCLIDE DE DUPIN
Dupin's
Cyclide, dupinsche Zyklide
 |
 |
 |

| Surface étudiée par Dupin en 1822, Darboux
en 1872 et Forsyth en 1912.
Du grec kuklos : cercle, roue et eidos : apparence. Charles Dupin (1784-1873) : économiste, mathématicien et homme politique français. REF : [Julia] p 425, [Dontot], [Hadamard] p 646, [d'Ocagne] p 204, [Valiron] p 478. Lien : Modèles mathématiques du Laboratoire de mathématiques de Besançon. |
1) Première définition : les cyclides
de Dupin (au sens strict) sont les surfaces, autres que les tores,
dont les lignes de courbures sont des cercles (exceptionnellement des droites).
On conjecture que ce sont les seules surfaces ayant une
double génération par des cercles, les deux familles de cercles
étant orthogonales.
2) Deuxième définition (directement équivalente
à la précédente) : ce sont les surfaces enveloppes
de sphères, de deux façons différentes.
Les sphères sont alors tangentes à la cyclide
suivant des cercles, qui sont les lignes de courbure.
On montre que les deux courbes focales (lieux des centres des sphères) sont des coniques situées dans des plans orthogonaux et telles que les foyers de l'une sont les sommets de l'autre; ce lieu constitue la focale de la cyclide. On nomme ces coniques les coniques focales de la cyclide.
Il y a alors deux cas : les coniques focales sont...
| ....soit une ellipse et une hyperbole, et la cyclide
est dite "ellipto-hyperbolique". Elle est alors bornée.
Les deux coniques jouissent de la propriété que pour tout couple de points I1 et I2 appartenant à l'une et l'autre, les deux plans tangents aux deux coniques en I1 et I2 contenant la droite (I1 I2) sont toujours orthogonaux. Visuellement, les deux coniques semblent donc se couper à angle droit. |
  |
| ... soit deux paraboles, et la cyclide est dite parabolique".
Elle est alors non bornée.
Même propriété visuelle que précédemment. |
 |
Les droites joignant deux points de chaque conique focale sont les normales à la cyclide (d'où l'explication de la propriété prcédente : les deux plans tangents précédents sont orthogonaux respectivement aux deux lignes de courbures en un point de la surface ; les lignes de courbure étant orthogonales, les plans le sont aussi).
A) Etude du cas ellipto-hyperbolique :
Les 4 cercles sections par les plans des deux coniques
sont appelés les cercles directeurs de la cyclide (ils la
définissent entièrement).
On obtient alors la cyclide "en anneau" 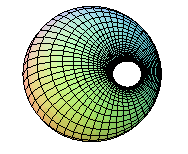 dans
les cas suivants :
dans
les cas suivants :
 |
 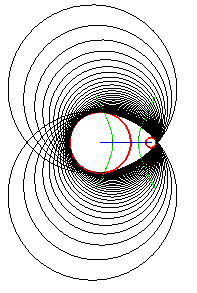 |
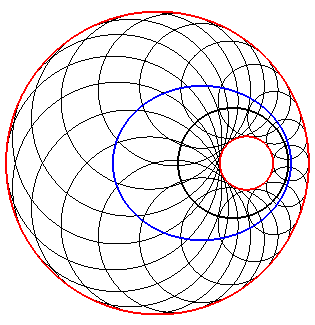
| Les cercles directeurs du plan de l'ellipse sont emboités, et
les sphères génératrices de la cyclide sont tangentes
extérieurement à ces cercles; l'ellipse est l'une des courbes
d'équidistance des deux cercles.
En noir épais, trace de la sphère orthogonale aux sphères génératrices (sphère de l'inversion échangeant les deux cercles directeurs). |
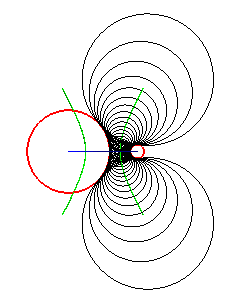
Les cercles directeurs du plan de l'hyperbole sont extérieurs l'un à l'autre. L'hyperbole est l'une des courbes d'équidistance des deux cercles. |
 |
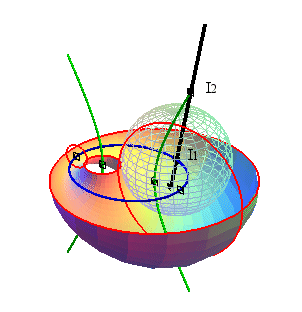  |
| Vue générale avec les 4 cercles directeurs et les 2 focales. | Toute normale en M à la cyclide rencontre l'ellipse focale en I1 et l'hyperbole focale en I2. Nous avons représenté la sphère de centre I1 passant par M qui est tangente à la cyclide, et à droite la sphère de centre I2. |
On obtient la cyclide "croisée interne"  dans
les cas suivants :
dans
les cas suivants :
 |
  |
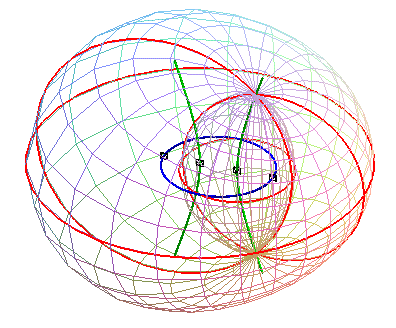 |
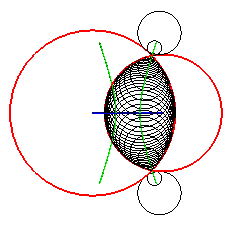
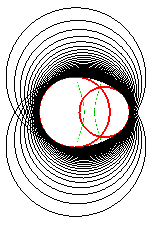
| Les cercles directeurs du plan de l'ellipse sont emboités, et les sphères génératrices de la cyclide sont tangentes intérieurement au cercle intérieur; l'ellipse est l'une des courbes d'équidistance des deux cercles. | Les cercles directeurs du plan de l'hyperbole sont sécants. L'hyperbole est l'une des courbes d'équidistance des deux cercles. |
Les cercles horizontaux sont emboités, les cercles verticaux sont sécants |
On obtient la cyclide en croissant double  dans
les cas suivants :
dans
les cas suivants :
 |
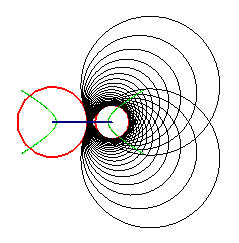 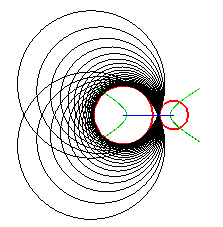 |
 |
| cercles directeurs du plan de l'ellipse sécants | cercles directeurs du plan de l'hyperbole extérieurs | les cercles horizontaux sont sécants, les cercles verticaux sont extérieurs |
La sphère centrée sur l'une des coniques
dont la cyclide est l'enveloppe est tangente à la cyclide en un
cercle qui est l'intersection de cette sphère avec le cône
de sommet le centre de la sphère et de directrice l'autre conique.
| Équations des Cyclides ellipto-hyperboliques :
Ellipse et hyperbole focales : Si 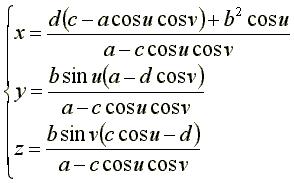 Équation cartésienne Surface quartique.bisphérique.rationnelle. Cas particuliers :
Les sphères tangentes sont les sphères de
centre |
B) Etude du cas parabolique.
| Cyclides paraboliques.
Paraboles focales : La paramétrisation cartésienne de la cyclide par la double famille des cercles de courbure est : Plans des cercles de courbure : La normale en M est la droite (I1I2) avec Équation cartésienne : Surface cubique sphérique rationnelle. Cas particuliers :
|
| La cyclide parabolique en anneau à cercles directeurs
isométriques est invariante
par retournement, le retournement échangeant les deux faces.
Après simplification par changement de repère,
l'équation de cette cyclide est Cf. la surface de Costa, et la surface d'Enneper, qui ont la même propriété. |
 |
3) Troisième définition : les cyclides de
Dupin sont les enveloppes des sphères tangentes (d'une certaine
sorte) à deux cercle-droite d'un plan, et centrées dans ce
plan. Les centres des sphères décrivent l'une des coniques
déférentes.
Il existe une deuxième génération
de ce type et les centres des 4 cercles obtenus (appelés les cercles
directeurs) sont les foyers des coniques focales associées.
4) Quatrième définition, équivalente à la précédente : les cyclides de Dupin sont les enveloppes de sphères de rayons R et centrées en M sur une conique de foyer F telles que la distance FM + R, ou la distance FM - R soit constante.
Ceci peut se visualiser dans le premier cas par l'ensemble des extrémités d'une ficelle tendue de longueur constante acrrochées à l'autre extrémité en F et passant par la conique.
Cette définition permet de voir facilement que les surfaces parallèles à une cyclide de Dupin sont encore des cyclides de Dupin, propriété qui a récemment fait redécouvrir ces cyclides pour des applications industrielles.
5) Cinquiéme définition : les cyclides de Dupin sont les enveloppes de sphères centrées sur une conique et orthogonales à une sphère fixe centrée sur l'axe focal de la conique. Cette définition montre que les cyclides de Dupin sont bien des cyclides. La sphère orthogonale est la sphère fixe de l'inversion laissant globalement invariante la cyclide.
6) Sixième définition : si l'on définit les cyclides de Dupin au sens large comme les surfaces dont les lignes de courbures sont des cercles ou des droites, ce sont alors les inverses de tores, de cones de révolution ou de cylindres de révolution.
La cyclide est en anneau ou croisées suivant que le tore correspondant a ces propriétés.
Elle est bornée et algébriques de degré 4 lorsque le centre d'inversion n'est pas sur le tore, non bornées et de degré 3 ou 2 sinon.
Les cyclides sont enveloppe de la famille des sphères inverses des sphères tangentes intérieurement au tore et de la famille des sphères inverses des sphères tangentes extérieurement au tore (idem pour cylindre ou cône).
avec le cas particulier du double croissant symétrique
(centre d'inversion situé à une
distance de
O
dans le plan Oxy)
Cette définition montre que les cyclides de Dupin
en anneau possèdent deux autres familles de cercles, inverses des
deux familles de cercles de Villarceau du tore
(cf. cet
article).
7) Septième définition : les cyclides de Dupin sont les surfaces enveloppes des sphères tangentes à trois sphères fixes.
8) Huitième définition : les cyclides
de Dupin sont les projections stéréographiques du tore
de Clifford (inclus dans S3).
Quelques modèles en plâtre, tirés
de ce site
japonnais :

cyclide en anneau |

cyclide croisée interne |

cyclide en croissant |

cyclide en croissant double |

cyclide parabolique en anneau dans le cas de deux cercles directeurs
isométriques.
|

cyclide parabolique en croissant double |
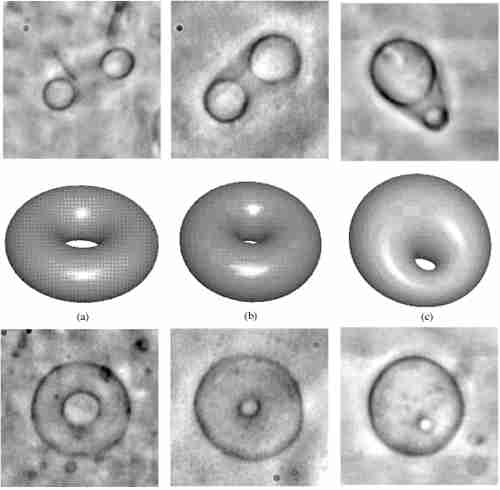
Les liposomes ont des formes de cyclides ; voir à surface de Willmore.


Voir ausssi cette
page réalisée par Alain Esculier.
| surface suivante | surface précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2013