Paramétrisation cartésienne : (où ). Équation cartésienne : . Surface algébrique rationnelle de degré 9. Première forme quadratique fondamentale : . Élément d’aire : . Deuxième forme quadratique fondamentale : . Courbure de Gauss : 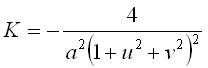. Courbure moyenne nulle (surface minimale). Rayons de courbure principaux : 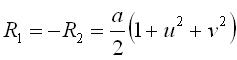. Aire de la surface obtenue pour  : . Les lignes de courbures sont les lignes de coordonnées associées à la paramétrisation en u et v (et elles sont planes). Les lignes asymptotiques sont obtenues en faisant .

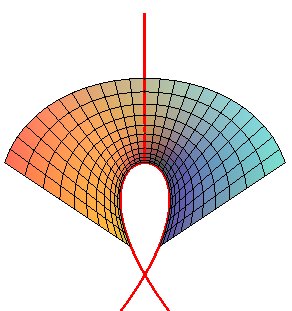
Surface d'Enneper, limitée au niveau de sa courbe d'auto-intersection.

La surface d'Enneper est la surface minimale obtenue en prenant  dans la paramétrisation de Weierstrass d'une telle surface : .
 
 

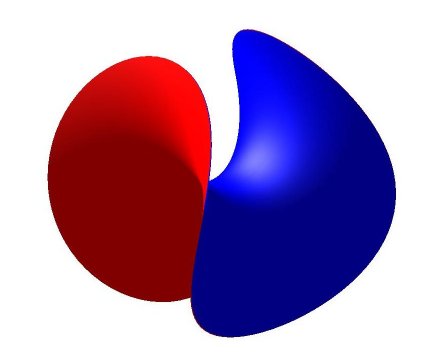
Elle peut être définie géométriquement comme l'enveloppe des plans médiateurs de deux points situés sur deux paraboles homofocales (i. e. des paraboles dont les plans sont perpendiculaires et dont le sommet de l’une passe par le foyer de l’autre ; comparer avec la définition de la cyclide de Dupin parabolique symétrique). Comme la configuration des paraboles homofocales, la surface d'Enneper est invariante par un retournement, ici d'axe x = y, z = 0 (échanger u et v dans la paramétrisation) qui échange les deux faces de la surface.  Dans la figure ci-contre, bien voir que les deux faces, la rouge et la bleue, sont identiques. Voir aussi la surface de Costa, qui a la même propriété.

 

Comme le montrent les formules , les projections sur xOy des lignes r = cte sont des hypotrochoïdes de paramètre q = 4 ; en particulier pour , on obtient un trèfle à 4 feuilles. Les courbes 3D : r = cte sont, elles, des coutures de balle de tennis.
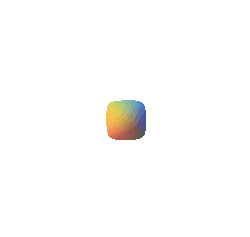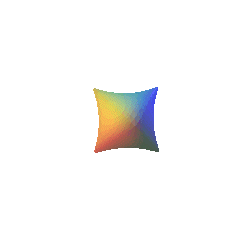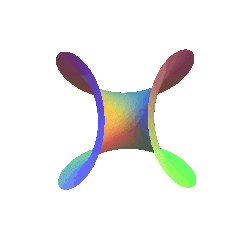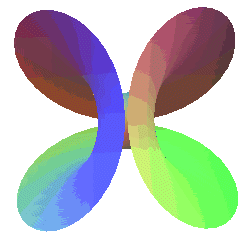On peut donc théoriquement matérialiser la surface d'Enneper en trempant une couture de balle de tennis :  dans une solution savonneuse de façon à obtenir un film de savon.	Réalisé avec povray par Alain Esculier

Cependant, il existe deux autres surfaces minimales s'appuyant sur le même contour, symétriques l'une de l'autre, et ayant une aire inférieure à la surface d'Enneper.  Ces deux surfaces sont intermédiaires entre les deux cylindres s'appuyant sur le contour représentés ci-contre, et la surface d'Enneper.
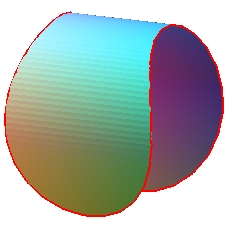Un film de savon physique suit l'une de ces deux surfaces et non celle d'Enneper ; une simple secousse permet d'ailleurs de passer de l'une à l'autre.	Photo Alain Esculier

 

Les deux sections de la surface d'Enneper par ses plans de symétrie (obtenues en faisant u = 0 et v =0 dans la paramétrisation) sont des cubiques de Tschirnhausen. Ce sont des géodésiques, ce qui fait que la surface d'Enneper est une surface de Björling associée à une cubique Tschirnhausen (surface minimale contenant cette cubique comme géodésique).

 

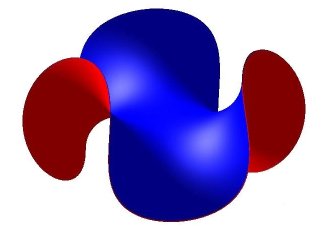
Si l'on prend  dans la paramétrisation de Weierstrass, on obtient la surface d'Enneper d'ordre n, de paramétrisation :  La surface d'Enneper classique est obtenue pour n = 2, et le cas n = 3/2 donne la surface de Bour. Les projections sur xOy des lignes r = cte sont des hypotrochoïdes de paramètre q = 2n, et ces lignes elles-mêmes sont à dilatation près des courbes de Capareda.

Cas n = 3 (cf la selle pour singe)

Cas n = 5

Comparer avec la surface de Scherk, autre surface minimale.
 

Surface d'Enneper d'ordre 3 en sculpture de glace.

Gravure de la  surface d'Enneper, par Patrice Jeener, avec son aimable autorisation.

Siège en surface d'Enneper

Enneper d'ordre 2 par Alain Esculier

Enneper d'ordre 4 par Alain Esculier

 

surface suivante

surface précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL  2011