Équation polaire :  avec n réel > 0. Courbe algébrique ssi n est rationnel. Aire pour e < 1 et n entier : . Cas particulier où l'abscisse curviligne s'intègre élémentairement : , soit  (donc pour e > 1, n <1) ,  qui donne pour abscisse curviligne dans ce cas : .

Les conchoïdes de rosace sont, comme leur nom l'indique, les conchoïdes de rosaces par rapport à leur centre.
Ce sont aussi les transformées de Brocard des limaçons de Pascal, par rapport à leur pôle.
La courbe est formée d'un motif de base symétrique par rapport à Ox obtenu pour  :
 

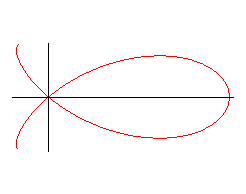
motif de base pour  e > 1

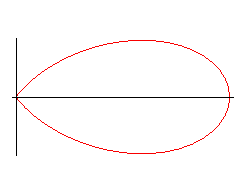
motif de base pour e = 1

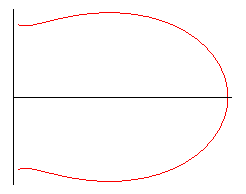
motif de base pour e < 1

transformé par toutes les rotations d'angle  pour k entier.
Lorsque n est rationnel de numérateur p, p rotations donnent toute la courbe.

Cas  e > 1, les rosaces de Troie :
 

n = 1 : limaçon de Pascal à boucle	n  = 2 : trisectrice de Ceva	n = 3	n = 4	n = 5
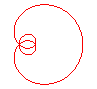
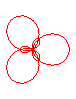
n = 1/2 : néphroïde de Freeth	n = 3/2	n = 5/2	n = 7/2	n = 9/2
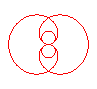
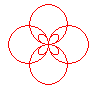
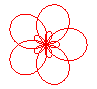
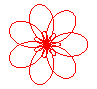
n  = 1/3	n = 2/3	n = 4/3	n = 5/3	n = 7/3
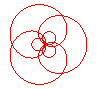
n = 1/4	n = 3/4	n = 5/4	n = 7/4	n = 9/4
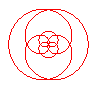
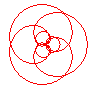
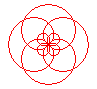
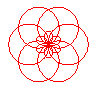
n = 1/5	n = 2/5	n = 3/5	n = 4/5	n = 6/5

Cas e = 1 :

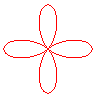
n = 1 : cardioïde	n  = 2 : oeuf double	n = 3	n = 4	n = 5
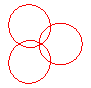
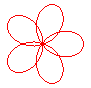
n = 1/2	n = 3/2	n = 5/2	n = 7/2	n = 9/2
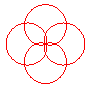
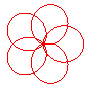
n  = 1/3	n = 2/3	n = 4/3	n = 5/3	n = 7/3
n = 1/4	n = 3/4	n = 5/4	n = 7/4	n = 9/4
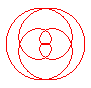
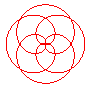
n = 1/5	n = 2/5	n = 3/5	n = 4/5	n = 6/5

Cas e < 1 :
Pour n = p / q, la conchoïde de rosace de paramètre n est une des projections possibles du noeud de bonnet turc de type (p,q) ; ses p sommets externes et ses p sommets internes forment un polygone régulier, et elle possède p(q – 1) points doubles.
Lorsque , la courbe posssède des points d'inflexion :
 

n = 1	n  = 2 : cacahuète	n = 3	n = 4	n = 5 étoile de mer
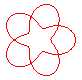
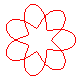
n = 1/2	n = 3/2 projection du noeud de trèfle	n = 5/2 projection du noeud 5.1	n = 7/2	n = 9/2
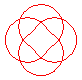
n  = 1/3	n = 2/3 projection du noeud de huit	n = 4/3 projection du noeud 8.18	n = 5/3 projection du noeud 10.123	n = 7/3
n = 1/4	n = 3/4 projection du noeud 9.40	n = 5/4	n = 7/4	n = 9/4
n = 1/5	n = 2/5	n = 3/5	n = 4/5	n = 6/5

Pour , la courbe est convexe. Le cas  donne donc de belles figures de polygones réguliers, croisés ou non avec des angles arrondis :
 

Les conchoïdes de rosace sont les vues de dessus des solénoïdes toriques.

Les inverses de conchoïdes de rosaces sont les polygastéroïdes.

Comparer aussi avec les folioïdes, et les courbes : .
 

Remarque : si l'on met une valeur absolue autour du cos, l'étoile de mer devient plutôt une fleur de tournesol :

La forme de la la conchoïde de rosace pour n = 3 et e < 1 : , avec une petite dilatation, n'a pas échappé à l'oeil des taupins qui l'ont dénommée pinochoïde :  A droite une variante plus élaborée : .

 
 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL  2017