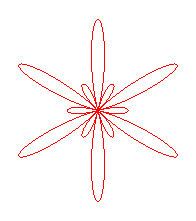
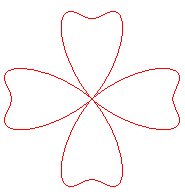
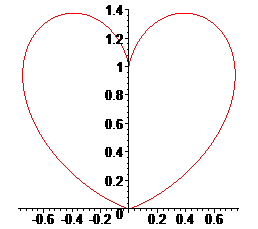| Trèfle de Habenicht (1895, Brocard
p. 100)
Équation polaire : Ci-contre, pour n = 3 et 4. Voir d'autres trèfles au bas de la page du quadrifolium. Ressemble aussi à l'oxalis triangularis. |
 |
............................
(Eugen Beutel : Algebraische Kurven, G.J. Göschen, Leipzig 1909-11)
Équation cartésienne :
Sextique non rationnelle.
....................
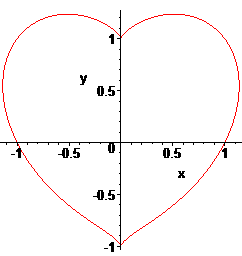Courbe trouvée par l'auteur à l'âge
de 16 ans pour sa petite amie...
Paramétrisation cartésienne : 
Biquartique
rationnelle.
Équation cartésienne :
x^8-x^6+27*x^4-27*x^2+12*y*x^6-12*y*x^4+42*y^2*x^4
+42*y^2*x^2+2*y^3*x^4+26*y^3*x^2+8*y^3+12*y^4*x^2+12*y^4+6*y^5+y^6=0
.......
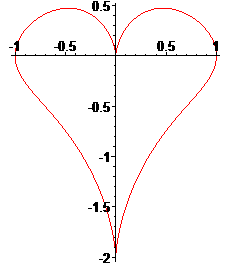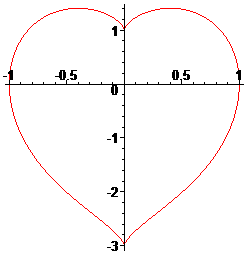
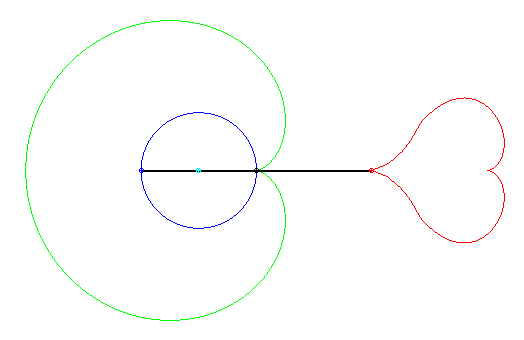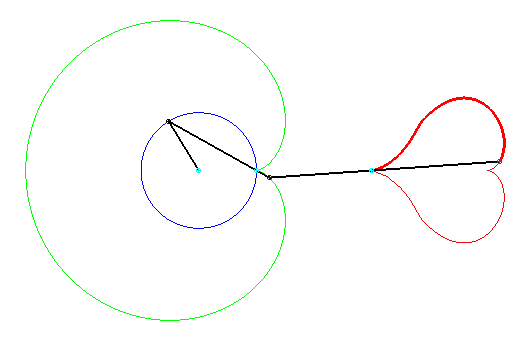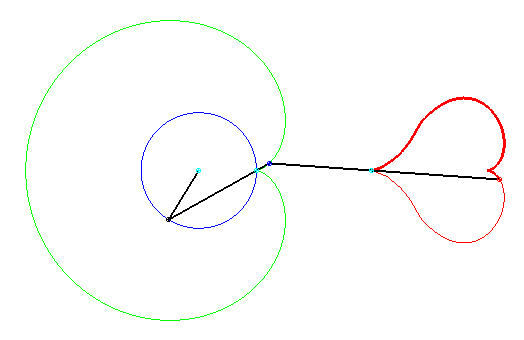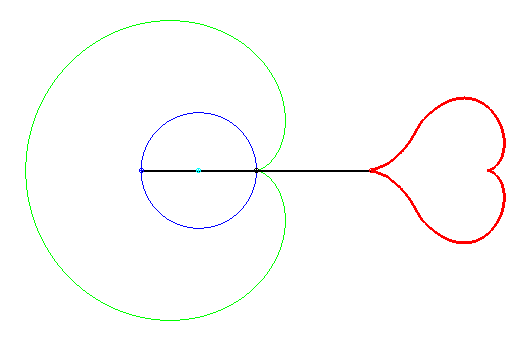
Équation polaire :
(portion d'une courbe qui se prolonge en fait de part et d'autre du point anguleux)
soit 
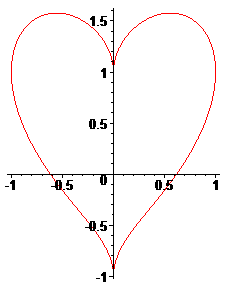
Ce coeur est formé d'une moitié de la réunion des deux quartiques en forme de huit :
et 
.
Donc, deux huits = deux coeurs !
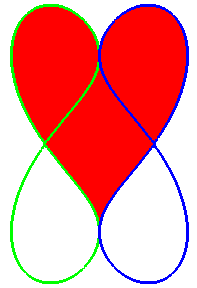
soit 
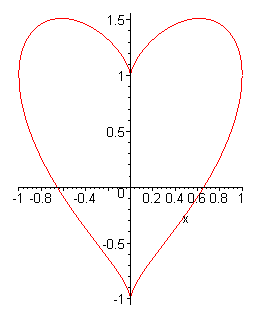
Equation cartésienne (biquartique non rationnelle) :
-108-36*y^2-448*x^2*y+112*x^2*y^2+405*x^4-112*y^3+12*y^4+66*x^4*y^2+224*x^4*y+128*x^2*y^3+24*y^4*x^2+
30*x^6+24*y^5+4*y^6+x^8-328*x^2+216*y+8*x^6*y+2*x^6*y^2+8*x^4*y^3+y^4*x^4=0
Voir à conchoïde de cercle.
Pour un répertoire des courbes en forme de coeur :
www.mathematische-basteleien.de/heart.htm
mathworld.wolfram.com/HeartCurve.html
Équation ponctuelle : 
Je ne connais pas les paramètres originels choisis
par Ehrahrt (qui affirmait qu'avec ces paramètres, la courbe coïncide
à la grosseur du trait de crayon près avec la forme de l'oeuf
obtenue par une étude statistique).
Ici, A = (0 ; 0), B = (0 ; 0,2), C = (0 ; 1), cte = 2,2.
Ehrahrt dénommait ces courbes "hyperellipses à 3 foyers" ; elles sont répertoriées dans ce site comme triellipses.
Voir d'autres oeufs à ovoïde.
Équation polaire : 
.
Équation cartésienne : 
ou 
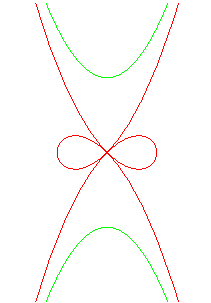
Paraboles asymptotes (en vert ) : 
.
Variante : 
,
soit 
dont
la partie en huit est la lemniscate de
Gérono.
Équation cartésienne : 
Équation cartésienne : 
.
Equation polaire : 
.
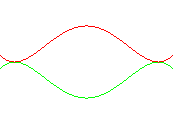
Équation polaire :
(à droite
).
Papillons de L. Sautereau (2010 )
Voir aussi le papillon de Cundy et Rollett.
Équation polaire :
Équation cartésienne :
A droite : 
Plus proche :
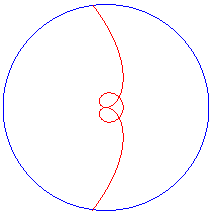
Équation polaire :
pour 
(ci-contre
avec a = p/2), plus le cercle 
.
Variante avec cercle asymptote à droite :
,
soit 
,
avec a = 1/2.
Prendre deux courbes du style
,
par exemple 
et faire tourner autour de l'axe de symétrie.
Voir aussi ici.
Cas n = 1/2, e < 1, e = 1, e > 1.
Cas n = 1, 3, 5, e < 1.
