1)
avec g strictement positive, C1
sur ]a, b[,
2)
concave sur [a, b] .
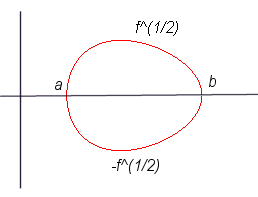
Profil de l'oeuf correspondant, courbe y²=f(x).
| surface suivante | surface précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
OVOÏDE
Ovoid,
Eifläche
| Autre nom : ovaloïde.
Vidéo youtube sur la recherche de l'équation du profil d'un oeuf d'oiseau : www.numberphile.com/videos/the-ultimate-egg-quation Article : scienceline.org/2021/11/a-new-equation-can-describe-every-egg/ |
Un ovoïde est une surface ayant la forme d'un
uf.
De façon très générale, on
peut donner la définition : surface de classe C1
frontière d'une partie convexe bornée de l'espace. Alors,
une surface fermée bornée de classe C1
dont tous les points sont elliptiques
(courbure de Gauss positive) est un ovoïde.
Pour se rapprocher plus d'un oeuf, on peut se restreindre
aux surfaces de révolution
définies par :
| Équation cylindrique : 1) 2) |

Profil de l'oeuf correspondant, courbe y²=f(x). |
Exemples :
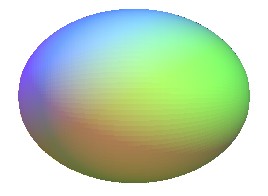
| l'ellipsoïde
de révolution ( |
 |
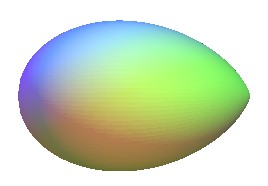
| l'ovoïde
de Képler, de profil un folium simple ( |
 |
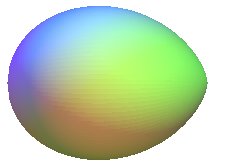
| l'ovoïde de profil un demi oeuf
double ( |
 |
| l'ovoïde de profil l'ovale de l'hyperbole
cubique à ovale, ou oeuf
de Hügelschäffer ( |
 |
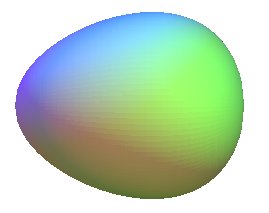
| l'ovoïde de profil l'oeuf
de Granville ( |
 |
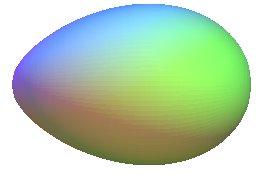
| l'ovoïde de profil la courbe
de Rosillo ( ci-contre avec a = 1, c = 2, d = 3 |
 |
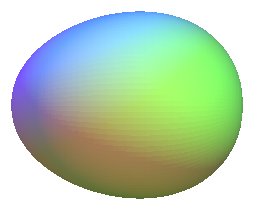
| A. de Quay propose |
 |
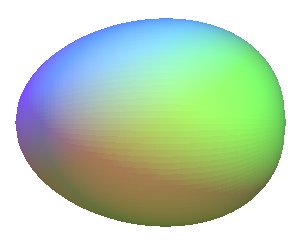
| Simon Cadrin propose |
 |
Voir aussi les ovales de Descartes, les oeufs d'Ehrhart, les courbes de la bielle de Bérard, les foliums droits.
Pour un répertoire des courbes en forme d'oeuf
: www.mathematische-basteleien.de/eggcurves.htm
| surface suivante | surface précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2016