
Anaglyphe à regarder avec des lunettes rouge (à gauche) et bleu (à droite).
| polyèdre suivant | polyèdre précédent | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
DODÉCAÈDRE RHOMBIQUE
Rhombic dodecahedron, Rhombendodekaeder
.
Anaglyphe à regarder avec des lunettes rouge (à gauche) et bleu (à droite). |
|
| Liens :
cm2.ens.fr/video/Dupas-polyedres/herbier/rhombique.htm mathematische-basteleien.de/rhombendodekaeder.htm |
| Étymologie | rhombique : du grec rhombos "losange". | ||||||||
| Autres noms | dodécaèdre rhomboïdal, rhombododécaèdre, ou granatoèdre (du latin granatus "grain, grenat", le grenat prenant des formes de dodécaèdre rhombique) | ||||||||
| Famille | polyèdre
semi-régulier de deuxième espèce
également : paralléloèdre, zonoèdre. |
||||||||
| Historique | solide connu d'Archimède (IIIe s. av. J.C.) ??? | ||||||||
| Dual | cuboctaèdre |
||||||||
| Faces | 12 losanges dont les grande et petite diagonale sont
dans le rapport |
||||||||
| Sommets | 8 sommets de degré 3, de code de Schläfli 43 et 6 sommets de degré 4 de code de Schläfli 44. | ||||||||
| Arêtes | 24 arêtes de longueur a ; angle dièdre : 120°. | ||||||||
| Patron |
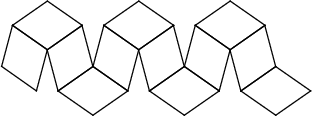 |
||||||||
| Graphe |
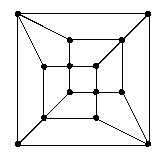 ou ou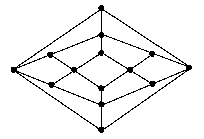 |
||||||||
| Diamètres | sphère inscrite : |
||||||||
| Mensurations | volume : coefficient isopérimétrique : |
||||||||
| Coordonnées
des sommets |
les 8 sommets de degré 3 formant un cube
: les 6 sommets de degré 4 formant un octaèdre : |
||||||||
| Equations des 12 plans faces | |||||||||
|
Equation du solide plein |
|||||||||
| Equation de la surface | |||||||||
| Constructions |
Voir aussi cette page. |
||||||||
| Polyèdres dérivés | Par troncature
des 6 sommets de degré 4 : dodécaèdre
rhombique tronqué.
Par adoucissement : 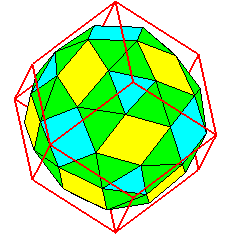
Stellations : voir ci-dessous |
||||||||
| Plans de symétrie | 9 | ||||||||
| Axes de rotation |
|
||||||||
| Groupe des isométries | = celui du cube |
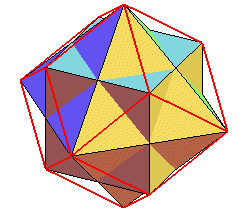 |
Le dodécaèdre rhombique plein est l'enveloppe convexe des sommets du cube et de son dual polaire, qui est un octaèdre ; les arêtes du cube sont alors les petites diagonales des faces du dodécaèdre, et celles de l'octaèdre les grandes. |
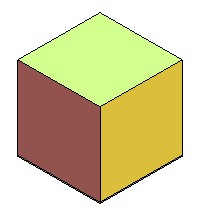
| Le dodécaèdre rhombique pose des problèmes
de vision dans l'espace, car lorsqu'on le regarde suivant une diagonale,
on a l'impression de voir un cube : le dodécaèdre plein est
en fait formé de 4 rhomboèdres
(que l'on prend pour des cubes).
Remarquons que chaque rhomboèdre a 3 faces libres et une face en commun avec chacun des 3 autres. Voir ici une superbe animation de cette décomposition. |
|
 |
| Si, à partir d'un tétraèdre
régulier de sommets les 4 points Ai= - on ajoute 6 sommets Bi = - on ajoute 4 sommets situés à distance
b
du
centre sur les demi-droites issues de O passant par les centres
des faces du tétraèdre, Ci
= |
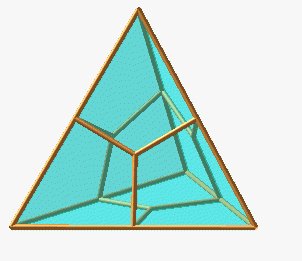
Cas a = 1.
|
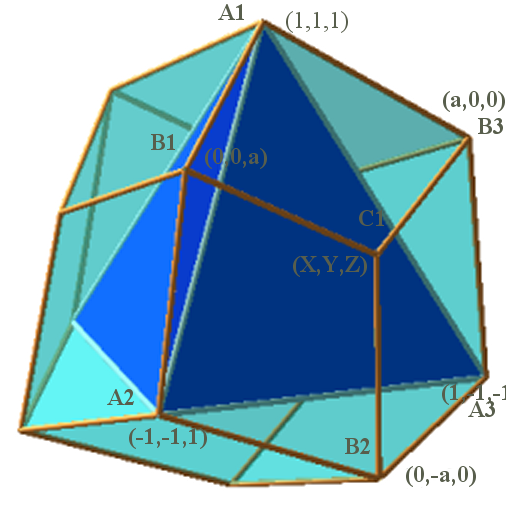
Cas |

Animation pour a allant de 1 à 3. |
| Les faces du dodécaèdre rhombique se regroupent en trois anneaux carrés de quatre losanges chacun, rouge, bleu, vert sur la figure ci-contre. De fait, comme vu dans les équations ci-dessus, le polyèdre plein est l'intersection de trois cylindres pleins à section carrée deux à deux orthogonaux disposés comme sur la deuxième figure. |
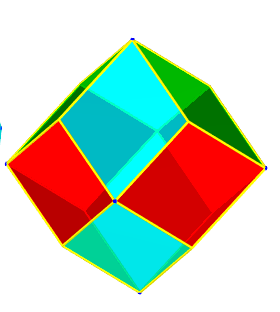 |
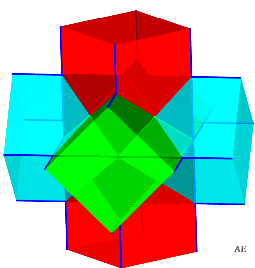 |
| Si l'on remplace les trois cylindres pleins à
section carrée par des cylindres de révolution, la frontière
de l'intersection possède la même structure que le dodécaèdre
rhombique ; mais les "faces" sont des portions de cylindres, et les "arêtes",
des portions d'ellipses.
Ce sont des cas particuliers de solides de Steinmetz. Figures d'Alain Esculier. |
 |
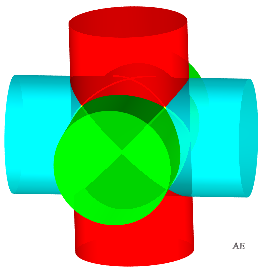 |
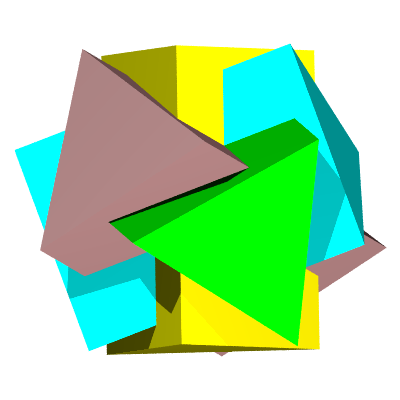
| L'intersection de quatre prismes triangulaires d'axes les quatre diagonales d'un cube, ou les quatre diagonales faciales d'un octaèdre, donne un polyèdre à 4x3 = 12 faces qui n'est autre que le dodécaèdre rhombique. Il y a cette fois quatre groupes de trois faces de même couleur. | 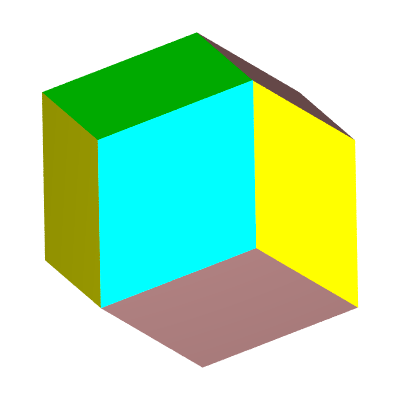 |
 |
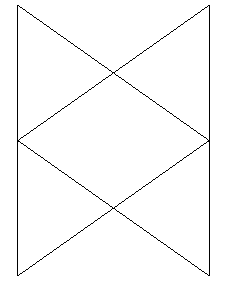
| Si l'on prolonge chaque face losange du dodécaèdre rhombique en un composé de deux triangles comme indiqué si contre, on obtient un polyèdre étoilé dénommé "première stellation du dodécaèdre rhombique", qui est toujours inscrit dans les 3 tubes carrés précédents. Les triangles sont isocèles non équilatéraux (base 4a/rac(3), côtés 2a). |
 |
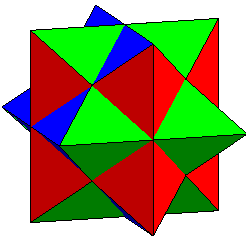 |
| On peut arranger les 2.12 = 24 faces triangulaires de
ce polyèdre en 3 groupes de 8 formant 3 octaèdres non réguliers
mais à faces isocèles "égales".
Chacun de ces octaèdres plein est l'intersection de deux tubes carrés plein. |
 |
 |
| Le dodécaèdre rhombique plein est réunion
de douze pyramides de sommets son centre.
Si l'on pose sur chaque face une pyramide égale à la pyramide intérieure, on obtient un polyèdre plein équivalent au polyèdre précédent. L'animation ci-contre montre de plus que les 12 sommets de ce polyèdre étoilé sont ceux d'un cuboctaèdre. |
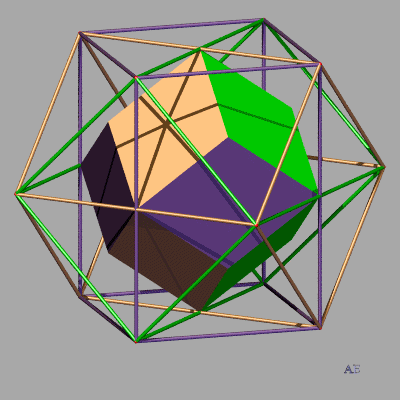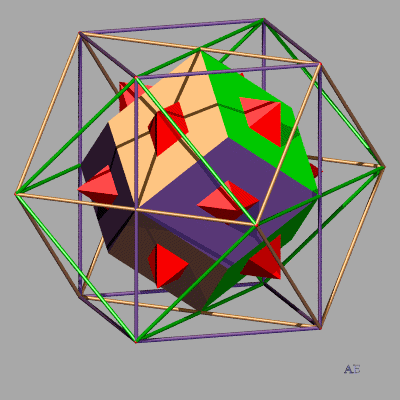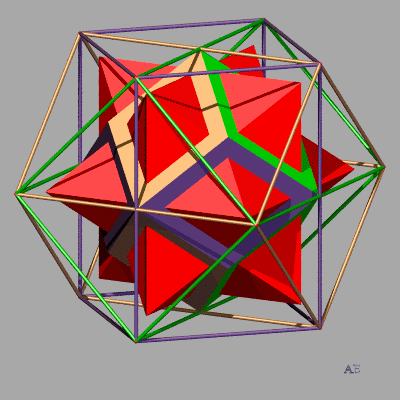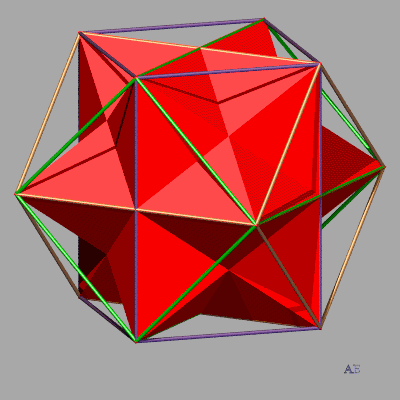 |
| On retrouve aussi cette stellation dans la célèbre gravure d'Escher dénommée "Chute d'eau", d'où son surnom de "solide d'Escher. |  |
 |
|
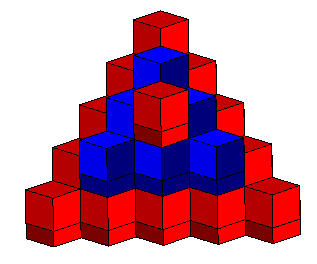
Construction d'un dodécaèdre rhombique
à partir de cubes, par la méthode de l'abbé René-Just
Haüy (voir aussi sa méthode de construction
de l'octaèdre).
L'unité de longueur étant le côté des petits cubes, on a à l'étape n en partant de l'étape 0 un cube de côté 2n + 1 surmonté de 6 pyramides de hauteur n. Cette construction tend vers un cube augmenté de 6 pyramides de hauteur la moitié du côté du cube, ce qui est bien un dodécaèdre rhombique. Le nombre de cubes à l'étape n en
partant de l'étape 0 vaut |
 |
Dans la construction similaire ci-contre où l'on
remarquera deux marches de même longueur. Elle tend aussi vers le
dodécaèdre rhombique.
Le nombre de cubes à l'étape n en partant de l'étape 0 vaut 1 (par convention), 7, 87, 335, 847, 1719, etc voir la suite A254473 de l'OEIS. |
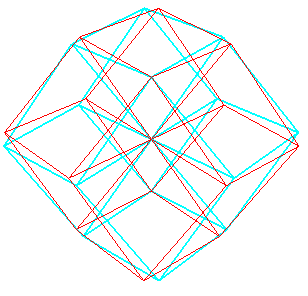
| Le dodécaèdre rhombique plein est une projection
affine de l'hypercube de dimension
4 plein.
Dans l'anaglyphe ci-contre, à regarder avec des lunettes rouge (à gauche) et bleu (à droite), on essaiera de distinguer les 6 parallélépipèdes projetés des 6 cellules cubiques de l'hypercube. |
 |
| Comme avec des cubes, on peut paver (c'est-à-dire
remplir sans trou ni chevauchement) l'espace avec des dodécaèdres
rhombiques.
Ci-contre, animation montrant l'agencement des douze dodécaèdres rhombiques accolés aux douze faces d'un autre dodécaèdre rhombique, centrés aux sommets d'un cuboctaèdre. Ce pavage de dodécaèdres rhombiques se déduit d'un pavage de cubes en formant dans un cube sur deux les 6 pyramides de base une face et de sommet le centre du cube, et en les accolant aux cubes contigus afin de former des dodécaèdres rhombiques. Voir aussi à également à paralléloèdre. |
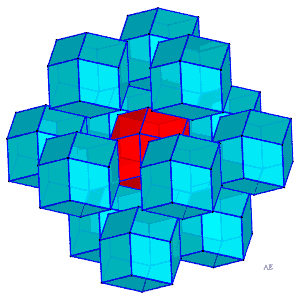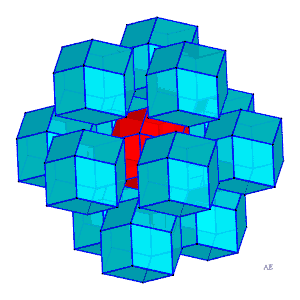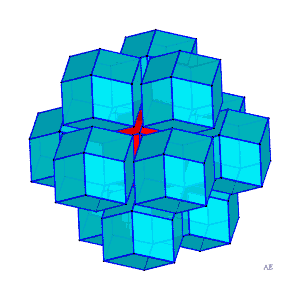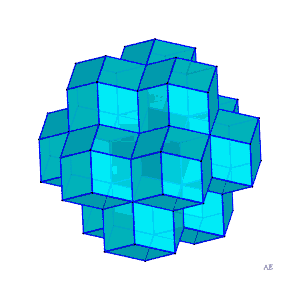 |
| Cette propriété de pavage provient du fait
que le dodécaèdre rhombique n'est autre que le "domaine fondamental"
(à savoir le domaine formé des points pour lesquels le noeud
le plus proche est le noeud considéré) d'un réseau
cubique
à faces centrées.
Ici, les dodécaèdres sont centrés
aux points de coordonnées
|
 |
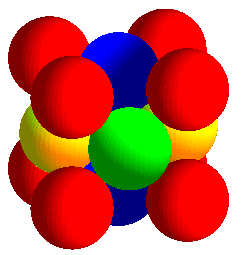
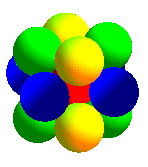
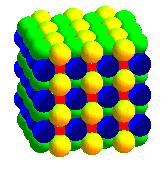
| Le réseau cubique à faces centrées
est obtenu à partir de deux réseaux cubiques simples, chaque
noeud de l'un étant au centre d'un cube formé par 8 noeuds
de l'autre.
On définit la densité d'un réseau
comme la limite du rapport du volume total des sphères identiques
tangentes centrées aux noeuds du réseau situées dans
un domaine donné, au volume du domaine, lorsque le domaine "tend"
vers l'espace entier.
|
   |
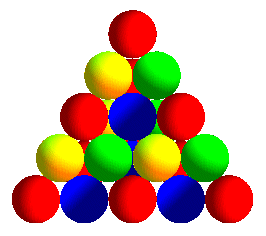
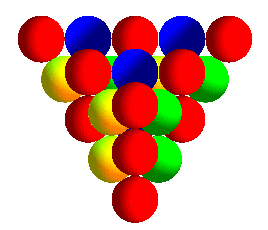
| Le réseau cubique à faces centrées
est celui qu'on obtient naturellement lorsqu'on range des oranges ou des
boulets de canon (que l'on parte d'une base carrée ou triangulaire).
|
 |
 |
| Le domaine fondamental du réseau
hexagonal compact, fournit un autre polyèdre qui pave l'espace,
combinatoirement équivalent au dodécaèdre rhombique,
mais dont les faces sont constituées de 6 trapèzes et 6 losanges,
d'où son nom de dodécaèdre
trapézo-rhombique.
Ce polyèdre n'est autre que le dual du pseudo-cuboctaèdre. |
 |
| Il existe une infinité de dodécaèdres
à faces losanges équivalents au dodécaèdre
rhombique semi-régulier, mais un seul autre à faces losanges
isométriques, le dodécaèdre
rhombique de Bilinski découvert en 1960, dont les faces
sont du même type que celles du triacontaèdre
rhombique (voir ici
la relation entre ces deux polyèdres). Celui-ci pave
également l'espace.
Photo : Gilles Josse. |
 |
| Les baies de grenade, à cause de la compression, tendent à s'empiler en réseau cubique à face centrée, ce qui explique qu'elles prennent la forme approximative de dodécaèdres rhombiques. |
| Les alvéoles d'abeilles ont la forme de prismes hexagonaux terminés par trois losanges faisant entre eux des angles de 120° ; ces trois losanges sont donc les 3 faces aboutissant à un sommet de degré 3 d'un dodécaèdre rhombique. On montre que cet angle de 120° est celui qui minimise l'aire de l'alvéole, de sorte que les abeilles résolvent un problème d'extrémum ! | 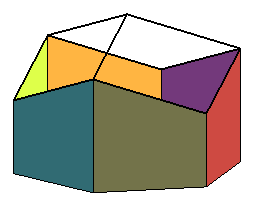 |
| Dans cette gravure tirée de "de divina proportione", intitulée "hexacedron elevatus vacuus", Léonard a placé manifestement des pyramides à faces équilatérales, ce qui ne donne pas exactement le dodécaèdre rhombique, mais donne une bonne idée de sa construction. | 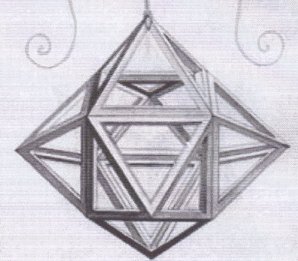 |
 |
Cristal de grenat grossulaire, en forme de dodécaèdre
rhombique.
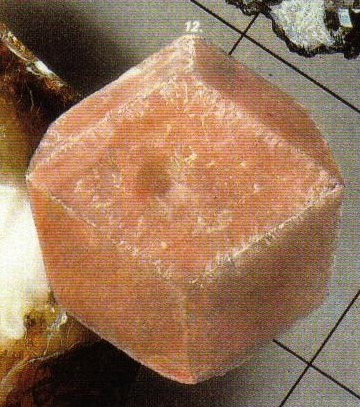 |
Voir aussi l'hypergranatoèdre, version 4D du dodécaèdre rhombique, et le triacontaèdre rhombique, qui est à la paire dodécaèdre-icosaèdre ce qu'est le dodécaèdre rhombique à la paire cube-octaèdre.


Animation réalisée par Alain Esculier
| polyèdre suivant | polyèdre précédent | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2023