polyèdre suivant polyèdre précédent courbes 2D courbes 3D surfaces fractals polyèdres

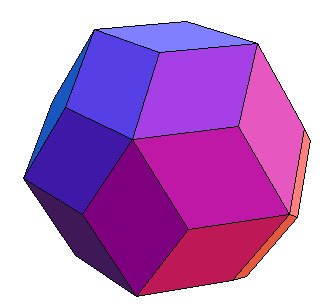
TRIACONTAÈDRE RHOMBIQUE
Rhombic triacontahedron, Rhombentriakontaeder

Étymologie du grec triaconta "trente" et  rhombos "losange" (polyèdre à trente faces en losange)
Autre nom triacontaèdre rhomboïdal
Famille polyèdre semi-régulier de deuxième espèce, ou polyèdre de Catalan
c'est aussi un zonoèdre
Historique connu de Képler en 1619 : , étudié par Catalan en 1862 
Dual icosidodécaèdre
Faces 30 losanges d'or (rapport des diagonales égal au nombre d'or) de petit angle =63° 26' et de grand angle =116° 34'.
Sommets 20 sommets de degré 3, de code de Schläfli 43 et 12 sommets de degré 5 de code de Schläfli 45.
Arêtes 60 arêtes de longueur a ; angle dièdre :  = 144°.
Patron et graphe
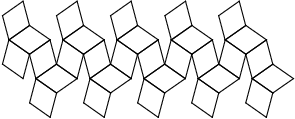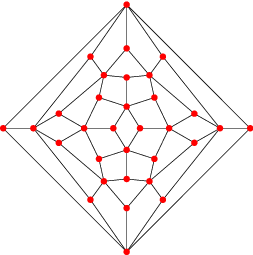Diamètres sphère inscrite :  ; intersphère (tangente aux arêtes) : ;
sphère circonscrite aux sommets de degré 3 : , 
aux sommets de degré 5 : .
Mensurations volume :    aire : .
Coordonnées des sommets les 12 sommets de degré 5 :  et permutés circulaires
les 20 sommets de degré 3 :  plus  et permutés circulaires
avec .
Équations des plans faces et permutés (soit 6 plans)  et permutés (soit 24 plans)
Constructions
dual polaire de l'icosidodécaèdre
dodécaèdre augmenté sur chaque face de 12 pyramides droites dont les angles des faces avec la base sont tels que chaque face est coplanaire avec celle de la pyramide voisine
icosaèdre augmenté sur chaque face de 20 pyramides droites dont les angles des faces avec la base sont tels que chaque face est coplanaire avec celle de la pyramide voisine
 
dodécaèdre tronqué aux arêtes (la troncature intermédiaire est le triacontaèdre rhombique tronqué)
icosaèdre tronqué aux arêtes
Voir aussi comment quelques traits sur un octaèdre tronqué donnent (visuellement) un triacontaèdre rhombique !
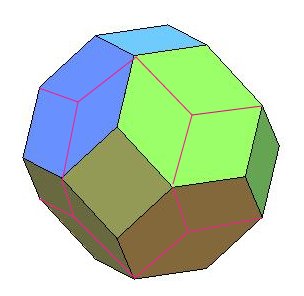Polyèdres dérivés triacontaèdre rhombique tronqué
icosèdre rhombique
Groupe des isométries  = celui du dodécaèdre

 
 
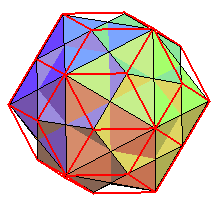Le triacontaèdre rhombique plein est l'enveloppe convexe des sommets du dodécaèdre régulier et de son dual polaire ; les arêtes du dodécaèdre sont alors les petites diagonales des faces du triacontaèdre, et celles de l'icosaèdre les grandes.

Le triacontaèdre rhombique est à l'icosaèdre et au dodécaèdre régulier ce qu'est le dodécaèdre rhombique au cube et à l'octaèdre.
L'intersection de 6 prismes décagonaux réguliers pleins dont les axes sont les 6 diagonales d'un icosaèdre (ou les diagonales faciales d'un dodécaèdre) forme un solide à 6x5 = 30 faces dont la surface est celle du triacontaèdre rhombique.

Tournés d'un vingtième de tours, les 6 prismes donnent l'hexacontaèdre trapézoïdal.

Figure par Robert March.

Voir aussi cette page sur les rosaces rhombiques.

Lien exterrne : www.georgehart.com/virtual-polyhedra/dissection-rt.html



 
 
 
 
polyèdre suivant polyèdre précédent courbes 2D courbes 3D surfaces fractals polyèdres

© Robert FERRÉOL 2024